Volition and Physical Laws

Jean E. Burns
Consciousness Research
1525 - 153rd Avenue, San Leandro, CA 94578
email: jeanbur@earthlink.net

The concept of free will is central to our lives, as we make day-to-day decisions, and to our culture, in our ethical and legal systems. The very concept implies that what we choose can produce a change in our physical environment, whether by pressing a switch to turn out electric lights or choosing a long-term plan of action which can affect many people. Yet volition is not a part of presently known physical laws, and it is not even known whether it exists -- no physics experiments have ever established its presence. (We will use the terms volition and free will synonymously in this article.) The purpose of this article is to make two points: first, that free will cannot be accounted for by presently known physical laws, and second, that if free will exists, any description of its effects in the physical world necessarily would constitute a radical addition to presently known physical laws.

The first point can be easily made. Presently known physical laws incorporate only the determinism of classical physics and the randomness of quantum physics, and neither of these are what is meant by free will. So they cannot account for it. One might think that this would end the discussion. However, Scott (1995) has pointed out that because of the complexity of biological systems, the properties of these can seem very different from those of relatively simpler physical systems, and he proposes that similarly, even though consciousness appears to have very different properties than those described by known physical laws, it may in fact entirely derive from these laws. Scott (1995) does not discuss the possibility of volition. However, volition (if it exists) is an aspect of consciousness. So if Scott's proposal is correct, it could be held that volition also derives from presently known physical laws. Scott makes his argument by presenting examples of experimentally determined biological properties which seem incompatible with those predicted by physical laws. However, we will see in the next section (Emergent Phenomena) that the apparent contradictions can be resolved on closer inspection. Therefore, there is no experimental evidence to support Scott's argument that properties of complex systems can be incompatible with the laws from which they ultimately derive. So there is no reason to think that we should not accept the above simple argument that presently known physical laws cannot account for free will.

With regard to the second point, any action of free will must necessarily produce a change in some quantity, such as energy or momentum, in the physical world. But any statement about, or even the acknowledgement of existence of, any such effects are part of the province of physics. So any such statement would constitute a radical addition to the known laws of physics.¹ This is true regardless of the nature of consciousness and free will themselves. One might conceive that these are entirely mental and not physical at all. Nevertheless, free will must produce physical effects (otherwise, it is not free will). Furthermore, it is likely that volition only acts when certain physical conditions are present (e.g., certain conditions characteristic of the brain) and produces effects of only a limited size, which become significant when they can be magnified by some physical process. After all, if volition could act anywhere (in the brain or out of it) to do anything, we should be able to lift a piano by sheer willing as easily as raising an arm. So this radical addition to physics would include a description of the physical characteristics and limitations associated with the effects of volition.

¹ The term "known laws of physics" is meant to include any of the theoretical machinery used in unified field theory and string theory, even though these subjects are in an unfinished state. This theoretical machinery uses the same basic concepts -- space, time, mass, interaction strength -- as the present body of physics and does not make any assertions about consciousness.

In discussing these points, we will review various proposals which link volition to physics through: classical physics and emergent processes; quantum mechanics; proposed new fields; and unified field theory. We will see in each instance a specific example of the first point, that presently known physics (including string theory and unified field theory) cannot account for free will (a point that most authors of proposals about free will do not emphasize). Nevertheless, we will see that these proposals offer gateways by which volition could exert its effects on the physical world, by working in association with, albeit with additions to, presently known physical principles.

When considering these proposals, it is important to also discuss conservation of energy. If free will produces physical effects which cannot be accounted for by physical forces, then its action does not conserve energy. And it has long been held that if free will does not conserve energy, it cannot occur. However, Mohrhoff (1999) has recently shown, by examination of the basic principles underlying energy conservation, that the physical world can consistently be regarded as an open system with respect to free will. His argument will be summarized herein.

It is also important to examine the problem volition has with respect to special relativity. One usually thinks of choices being made in the present moment, with the future not yet determined. However, as we will discuss, special relativity does not permit a universal ordering of events, such that they can be divided into past, present and future. While this is not necessarily an insurmountable obstacle to the existence of volition, it presents conceptual difficulties which should not be ignored. We will also discuss an alternative to special relativity, the theory of universal time of Moon, Spencer et al. (1989b), which permits the universal ordering of events and thereby circumvents the latter problem.

Some physicists have suggested that we are now reaching the end of physics, with all basic principles in view (Horgan, 1997; Lindley, 1993), as will be summarized herein. However, if physics is now reaching completion and no new principles are to be added, including any which could account for physical changes in the brain as the result of mental intention, then free will must be an illusion. In other words, all of our actions would result solely from either deterministic actions or quantum randomness. Deterministic actions would not necessarily be predictable because the brain processes involved might be chaotic and very sensitive to conditions in the surrounding environment. But they would be deterministic all the same. So, for some curious reason, we would have an experience of being able to influence our environment and think we are making plans and agonizing over decisions. But in fact we would have no power to change anything at all, and our actions would be determined solely by randomness and/or minute electrochemical changes in the brain caused by our environment, interior programs, or happenstance. Intuitively, most of us feel that we do have free will. But it should be understood that, with respect to presently known physics, the assertion that it exists is a radical statement.

In order to have a specific definition of free will for our discussion, we will borrow one used in philosophy: Free will is an influence on physical events which corresponds with mental intention and causes a physical change which would not otherwise occur in identical physical circumstances.² The latter definition is basically the same as that of Griffin (1998) for "freedom" and Seager (1995) for "causal power of consciousness." Not all philosophers, however, agree that free will exists. Kim (1993) and McGinn (1991), for instance, hold that because presently known physics does not allow for free will, it cannot exist.³ In a similar vein, some scientists and philosophers, such as Crick (1994), Dennett (1984), and Searle (1992), identify free will with the action of brain processes, as determined by the laws of physics.^4,5 None of these researchers mention the possibility that any additions might be made to the laws of physics. It follows that free will, as they present it, is an illusion, an experience which has no causal efficacy.

Of course, it is possible to investigate the brain processes associated with the experience of volition without taking a stand as to whether volition genuinely exists or is simply an illusion. Some neuroscientists explore the neural basis for this experience, yet in their articles make no specific comments about the physics associated with this experience. In these cases no stand is taken as to whether volition actually exists.

We should note that proposals for consciousness and volition have been made in the context of a variety of ontological viewpoints, including physicalism (as an emergent phenomenon), dualism, idealism and panpsychism (Griffin, 1998; Seager, 1995; see Burns (1990) for a summary of other views). The choice of ontological viewpoint seems somewhat a matter of personal preference in that proposals for particular models, e.g., the association of volition with the ordering of quantum randomness, have been made within a variety of ontologies and no experimental test is known which could distinguish between emergent physicalism, say, and some other ontology (Burns, 1991, 1996). So we will not discuss ontological matters to any great extent herein. Rather, we are focusing on the physical effects that volition can produce.

Emergent Phenomena

The view that consciousness arises out of physical phenomena which have certain special characteristics, such as a suitable level of complexity, is often called emergentism. The idea of emergent properties is used in two ways with respect to physics, and we need to understand the difference between them. First, if particles or systems are combined, new properties may appear as a result of the combination, even though the physical laws which govern them are the same. For instance, if a proton and an electron are combined, the result is a hydrogen atom, which has quite different properties than the original free particles. Another example is quantum nonlocality. In order for this property to be exhibited, a system of particles must be correlated. (The latter might occur, for instance, because the particles have a common origin and the correlation is required by a conservation law.) If particles are correlated, they show properties they would not otherwise have. Nevertheless, these nonlocal properties are determined by known laws of physics.

² If it is held that free will acts through the ordering of randomness, the definition would have to be extended to sequences of acts across time and/or assemblages of acts for a number of people, rather than only applying to an individual event, and would include provision for a test which would distinguish between random and non-random sequences of possibilities. See the section Quantum Randomness for further discussion.

³ Kim (1993, p. 107) says, "Mental causation ... is epiphenomenal causation, that is, a causal relation that is reducible to, or explainable by, the causal processes taking place at a more basic physical level." He also insists that the physical world is causally closed.

⁴ Searle (1992, pp. 111-112) says, "[C]onsciousness is ... an emergent feature of certain systems of neurons in the same way that solidity and liquidity are emergent features of systems of molecules." He adds that, in his view, consciousness does not have causal powers beyond what can be explained in terms of neurons.

⁵ Dennett (1984, p. 137) says, "[P]eople are physical objects which, like atoms or ball bearings or bridges, obey the laws of physics [and] are not ... more complicated than anything else we know in the universe ..." He leaves open the possibility that quantum indeterminacy could provide a path for volition, but includes no discussion of the distinction between randomness and choice (see text herein). If one accepts that distinction, then free will, as Dennett presents it, cannot exist.

We can call the above examples ordinary emergence, i.e., in these cases the new properties are determined by known laws of physics. In the above examples, the new properties can be predicted in detail from the laws of physics. However, as Scott (1995) has discussed, there are also many examples of systems for which it simply is not practical to predict their detailed actions even though if it presumed that their properties follow from the laws of physics. For instance, in a chaotic system events are so sensitive to the parameters that determine its action that any minor, unmeasurable fluctuation in these can change its observed behavior. A tornado provides an example -- although the general characteristics of tornadoes are understood, it is not possible to make precise predictions about when, where, or whether one will occur. Also, most phenomena in chemistry and biology involve such complex descriptions in terms of their molecular constituents that it is not practical to trace them back to the fundamental laws of physics. Rather, most descriptions of chemical and biological processes are determined experimentally and are phenomenological. Such cases can also be considered examples of ordinary emergence because the properties of such systems are presumed to follow from basic physical laws.

On the other hand, one can conceive that in some special situation, new properties might emerge which are not determined by known physical laws, and we can refer to this as radical emergence.⁶ As Chalmers (1996) has discussed extensively, the existence of consciousness cannot be accounted for by physical concepts.⁷ Therefore, if consciousness is to be accounted for by physicalism, it must be considered to arise through radical emergence. The basic physics involved in Chalmers' argument is very simple and can be summarized as follows. If something is to be explained in terms of physical concepts, then it must be possible to trace the way in which it relates to these concepts. But physics is about such things as mass and velocity, and no way is known to trace the fact that we have experience back to these physical qualities. So the assertion that it can be done is not justified.⁸

⁶ Previous to the 1990's the distinction between ordinary and radical emergence was not a major issue. The simple term emergence was generally used, and its meaning was similar to what is herein called radical emergence (see Kim, 1993). Nowadays in philosophy the distinction between the two forms of emergence is often specifically acknowledged. The term emergence then refers to any sort of emergence, including ordinary emergence, and the term radical emergence is roughly similar to the term used herein. However, the exact meaning of the latter term varies from author to author (see Seager, 1995; Silberstein, 1998).

⁷ Others have also made this basic point, e.g., Libet (1987).

⁸ Strictly speaking, Chalmers addresses the issue of whether consciousness can be explained in terms of physical facts, whereas in the text above we are interested in whether it can be explained in terms of physical concepts. However, the line of argument is the same in each case.
Chalmers (1996, p. 104) says, "[P]roponents of reductive explanation ... will have to give us some idea of how the existence of consciousness might be entailed by the physical facts. While it is not fair to expect all the details, one at least needs an account of how such an entailment might possibly go. But any attempt to demonstrate such an entailment is doomed to failure. for consciousness to be entailed by a set of physical facts, one would need some kind of analysis of the notion of consciousness--the kind of analysis whose satisfaction physical facts could imply-and there is no such analysis to be had."

However, Scott (1995) disagrees with Chalmers, in that he proposes that consciousness can be accounted for by ordinary emergence.⁹ So before turning to the relationship of volition and emergence, we should first consider Scott's argument. Scott points out that the characteristics of phenomena which arise in ordinary emergence can appear very different from those of the underlying parts and can even appear to contradict the underlying physical laws. As an example, Scott cites the Hodgkin-Huxley equations, which describe ionic currents along a neuron membrane. To understand this example, we need to know that all dynamical equations of physics (those which describe the interactions of fields and particles) have the mathematical property that they are time reversible, i.e., for any solution which describes a particle traveling forward in time, there is an additional solution which describes a particle traveling backward in time (Zeh, 1989). (Physicists do not take this to mean that particles actually, or necessarily, travel backward in time, but this is a characteristic property of these equations.) Scott points out that the Hodgkin-Huxley equations are not time reversible, and in this respect they are not compatible with the basic dynamical laws of physics. Thus, Scott argues, the physical processes described by these equations are entirely determined by the dynamical laws, and yet they can be shown to be incompatible with these laws. In that case, he argues, surely it is no great conceptual stretch to suppose that consciousness is entirely determined by physical laws and that we don't recognize the relationship because of the immense complexities of the processes involved.

In considering this argument, we should know that the Hodgkin-Huxley equations Scott cites are not at all unique in lacking time-reversibility. Rather, there are numerous processes, such as heat flow, diffusion, and chemical reactions, which have this characteristic, and they are referred to as thermodynamic processes. Physicists have long recognized the disparity between the time dependence of dynamical and thermodynamic processes (Davies, 1974; Prigogine, 1980; Zeh, 1989). A variety of solutions have been proposed which can resolve this disparity, and there is no general agreement as to which is the best one. However, all these solutions take into account, in one way or another, additional factors beyond merely the internal dynamics of the particles in the system. For instance, Zurek and Paz (1994) have proposed that the irreversibility of thermodynamic processes can be accounted for by effects of the environment.¹⁰

⁹ Scott (1995) at no time proposes radical emergence, i.e., emergence which depends on a new principle of physics, and all of his examples are of ordinary emergence. Also, he states, "As a natural scientist, I agree that all is constructed from the particles and fields of physics ..." (p. 168). Thus when he asserts that consciousness is an emergent phenomena, he refers to ordinary emergence.

¹⁰ An older explanation, presented in many textbooks, is that thermodynamic equations can be derived by averaging over dynamical processes within the system. However, no suitable method of averaging has ever been found which can account for the difference in time dependence (Zeh,1989).
Zurek and Paz (1994) have shown, using a simple system as an example, that thermodynamic effects, such as entropy increase, can be accounted for by random effects of the environment on a system. Thus the difference in form between dynamical and thermodynamic equations arises because the latter incorporate the average random effect of the environment. It is also necessary to account for entropy increase in an isolated system. However, the randomizing effect of vacuum radiation, amplified in molecular interactions, is sufficient to bring a thermodynamic system to equilibrium within a few collision times (Burns, 1998). Thus, in an isolated system, vacuum radiation acts as the "environment."
Prigogine and co-workers have shown that in highly unstable systems, thermodynamic effects derive from the instability of the system (Prigogine, 1997; Petrosky & Rosenberg, 1997). (Their explanation of irreversibility involves using a mathematical framework which is somewhat extended beyond that used for dynamics, and by implication involves an addition to physical laws (see also Prigogine, 1980). However, this mathematical extension has nothing to do with consciousness.)
It has also been proposed that the irreversibility of thermodynamic processes can be accounted for by the expansion of the universe (Zeh, 1989), but no explanation has been made of how this expansion, which is uniform over space, could account for differing thermodynamic effects in local systems.

Thus this difference in time dependence can be explained when all relevant factors are taken into account, and there is no reason to suppose that any physical process, including the ionic currents described by the Hodgkin-Huxley equations, acts in contradiction to the basic laws of physics. Therefore, there is no example of a physical process which could lead one, by analogy, to conclude that characteristics of consciousness could be utterly unlike those described by physical laws and yet that these characteristics could be a product of these laws.

Thus if consciousness arises from the physical world, it must do so by radical emergence. In other words, a new physical law (or laws), which would include concepts specific to consciousness, must be involved. It has been proposed that consciousness arises from matter which is sufficiently complex and appropriately organized (Bateson, 1979; John, 1976). Similarly, functionalism asserts that consciousness arises when sufficiently complex calculations are done, such as those in the brain. All these proposals must necessarily involve radical emergence.

Volition is an aspect of consciousness, so if consciousness arises from the physical world, volition presumably does also. In any case, regardless of whether consciousness and volition might be considered physical or non-physical, the physical effects produced by volition cannot be explained by presently known physical laws because these laws encompass only determinism and quantum randomness. Also, we do not mean by volition a process of which we simply are ignorant of the details. As noted earlier, it is not possible to know all the specific details governing a tornado, but we do not ascribe free will to it on that account. So there is no way, conceptually, to trace the physical effects of volition back to presently known laws.

None of the authors cited above (Bateson, 1979; John, 1976; Scott, 1995) discuss the issue of volition. However, Sperry (1983) has proposed that both consciousness and free will emerge from the fluctuating physical patterns which make up cognitive processing in the brain. Sperry did not specifically discuss the distinction between ordinary and radical emergence, but his views are consistent with the idea of radical emergence.¹¹ However, for the reasons given above, this proposal (or any proposal that volition emerges from the physical world) would constitute a major addition to conventional physics.

¹¹ Sperry (1983) affirms numerous times that mental events arise out of the physical world, but says, "I hold subjective mental phenomena to be primary, causally potent realities as they are experienced subjectively, different from, more than, and not reducible to their physicochemical elements." (p. 79) He also states that mentalism (his view) is the antithesis of physicalism and materialism (p. 79).

Quantum Randomness

Present day physics incorporates the idea of randomness in quantum processes, and it is possible that volition acts by selecting among the possibilities in a random event. There are two types of randomness for which this action could occur: collapse of the wave function and quantum fluctuations within the limits of the uncertainty principle. We will discuss each type in turn.

First, however, we should understand the difference between a sequence in which events occur randomly and one in which they do not. Random sequences have several basic properties. In the first place, each possible alternative for an event in the sequence has a certain probability, such that each possible event occurs a certain number of times (on the average) in a given number of events. For instance, if you shuffle a deck of cards and then draw a card at random, the probability that you will draw the ace of hearts (say) is 1 in 52.

Another important property is that each event occurs independently of past history. It follows from the mathematics that the probability of a certain type of event occurring twice in a row is the square of the probability that it occurs once. Let us suppose that after drawing the above card, you put it back in the deck (to keep the total number of cards constant), shuffle and draw again. Then the probability that you will draw the ace of hearts twice in a row is 1/52 x 1/52 = 1/2704, or one chance in 2704. Similarly, if you do the same thing three times, the chance of getting the ace of hearts three times in a row is 1/52 x 1/52 x 1/52 = 1/140,608, or one chance in 140,608.

Let's apply this idea to human behavior. Suppose you are bemusedly considering the possibility that you will stand up, go to the middle of the room and recite a nursery rhyme aloud. For the sake of putting a number on this, let's suppose that the probability you will actually do this is 1 in 100. In other words, if it crosses your mind 100 times, you might do it once.

Therefore, if your behavior is determined randomly each time the thought of reciting the nursery rhyme crosses your mind, the probability that you will recite it twice in a row is 1/100 x 1/100 = 1/10,000, or one in ten thousand. Similarly, the probability that you will do it three times in a row is 1/100 x 1/100 x 1/100 = 1/1,000,000, or one in a million.

Suppose, in the interests of establishing the plausibility that you have free will, that you recite the nursery rhyme three times in succession. This behavior cannot in itself prove that you have free will because you might actually be carrying out some improbable random series or an odd, but deterministic, brain program. However, the example shows the contrast between a random sequence, for which reciting the nursery rhyme three times is very improbable, and a volitional sequence, in which you can recite it three times whenever you want. If volition is accomplished through selecting alternatives in an originally random process, the sequence of results can be very different from what the original random process would typically produce. A further principle beyond randomness would be needed to account for such results, and this principle would be a radical addition to present-day physics. Any change which would make an originally random process less random can be called an ordering of that process, so this proposed principle can be referred to as the ordering of quantum randomness.

It is sometimes suggested that volition should produce the same average results as a random process, presumably to make it resemble more closely the original process. Such an averaging might be supposed to apply to a single individual through time, or across groups of individuals. But either seems an unreasonable limitation of the concept of volition, as we can see by the following examples. Suppose this constraint applies to a single individual through time. Suppose you recite the nursery rhyme three times today. Then, even if you consider the possibility every day for each of the following one million days, or about 3,000 years (if you live that long), the constraint that the number of times you do it must conform to the random average would prevent you from doing it again. On the other hand, suppose this constraint applies to groups of individuals. Then if you recite the verse three times today, there are a million other people (minus one) who won't, not because of their individual preferences, but because you have already done it. It seems simpler to acknowledge that an entirely new principle would be needed.

Collapse of the Wave Function

It is not known whether there is such a phenomenon as collapse of the wave function, and some interpretations of quantum mechanics, such as that of Bohm and Hiley (1993), say there is no such thing. Also, assuming that collapse does occur, the means by which it happens are not known (Wick, 1995). However, some physicists (e.g., Goswami, 1993; Stapp, 1996; Walker, 1975) have proposed that collapse is produced through the action of consciousness. In that case, even though collapse is ordinarily a random process, volition could act to select among random quantum mechanical alternatives.

However, we should follow this line of thought further and ask what physical characteristics or limitations such a process would have in the brain. In order for wave function collapse to occur, the system the wave function describes must have quantum coherence. Thermal motions, such as would occur in a brain at room temperature, would seem to preclude quantum coherence at the cellular level of the brain. But coherence may occur in some cellular substructures, such as microtubules (Penrose, 1994).¹² Thus some magnification process would be needed in order that collapse to a particular state of a microtubule (say) would produce an effect at the level of neural processing. If volition effects are produced in subcellular structures, and have to be magnified, this can explain why the volition process itself is not readily observable in the brain. On the other hand, this does not explain why the volition process cannot directly affect macroscopic quantum coherent phenomena, such as superconductors. So if volition acts via wave function collapse, there must be additional physical specifications which constrain its action. Such specifications would make further additions to presently known physical laws, beyond even the statement that volition can produce the ordering of randomness.

Quantum Fluctuations

It is not possible to simultaneously measure both position and momentum of a particle within the limits specified by the uncertainty principle (Jammer, 1974). Furthermore, according to the Kochen and Specker/von Neumann theorem, position and momentum cannot simultaneously have definite values within these limits even theoretically (Mermin, 1990). However, as Abbott and Wise (1981) have shown, the very fact that these variables are limited by the uncertainty principle means that a particle can be described as constantly undergoing quantum fluctuations within these limits. The average (root mean square) values of these coordinates can be simultaneously specified, even though the individual coordinates cannot be, and are the same as for brownian motion (Abbott and Wise, 1981).

These fluctuations can be thought of as either occurring spontaneously, as in the above description, or as being induced by the random effects of vacuum radiation (Burns, 1998). The effects of vacuum radiation are ordinarily thought of as either being very small (e.g., the Lamb shift) or only occurring in unusual circumstances (e.g., the Casimir effect). However, it has recently been shown that such fluctuations can account for entropy increase in thermodynamic systems (Burns, 1998) and thus produce effects which are significant even at the macroscopic level. Thus we might conceive that volition consists of the ordering of these fluctuations.¹³

¹² Penrose (1994) holds that quantum coherence and wave function collapse are necessary but not sufficient conditions for consciousness. He makes no statements about physical characteristics associated with free will, however, merely saying that he believes free will exists (p. 39-40) and that it appears to be involved in questions about the nature of time (p. 387).

¹³ Because quantum fluctuations can be attributed to the action of vacuum photons, volition could be viewed as acting to order their random motion.

The fact that these fluctuations must occur within the limits of the uncertainty principle limits the magnitude of the effects they could produce. Wilson (1999) has analyzed the various physiological means by which volition could be carried out in the brain within these limits, and has shown that it cannot act by shifting the coordinates of any single molecule or molecular component. For instance, he has shown that the piece of protein molecule which forms a gate to a sodium channel cannot be moved for a sufficient length of time, within these limits, to permit sodium ions to pass through the channel. One might conceive that volition acts to simultaneously order the thermal motions of a number of water molecules near the protein gate, with the change in motion of each molecule being within the limits of the uncertainty principle. No quantitative calculations have presently been made to show how many water molecules (undoubtedly a very large number) would need to be simultaneously ordered in order to open an ion gate. However, such process would be a radical addition to known physical laws.

New Particles or Fields

Could volition be a new particle or field? In quantum mechanics each interaction can be viewed as either a field or a particle (e.g., the electromagnetic field corresponds to a photon), so we have no loss of generality by considering only fields. However, the problem with considering volition to be a field comparable to other physical fields is the following. This supposed new field would have to interact with electric charges, because all cognitive processing in the brain takes place via electric currents and accompanying potential differences. Thus it would be a new constituent of the electromagnetic field. But the latter field is known to be unified with the weak force, to form the electroweak field. The nature of the unification is theoretically understood, and the theory is experimentally verified. It would not be consistent with known data to add another constituent to the electromagnetic field. So this possibility can be ruled out.

The above difficulty can be avoided if consciousness is considered to be a mental phenomenon, a different type of entity than physical fields, which simply has field-like characteristics. Libet (1994) has proposed such an entity, which he calls a "conscious mental field" or "CMF", and has proposed that conscious experience represents information from different parts of the brain via these field-like characteristics. The CMF would also be responsible for volition.

However, even if consciousness is assumed to be entirely mental, if it has physical effects, the characteristics of these effects would constitute an addition to physical laws. For example, in split brain patients, the conscious experience of the left hemisphere does not incorporate information from the right hemisphere. Sperry (1977) has suggested generalizing this finding to conclude that intact neural connections are necessary for information represented in the brain to be incorporated into conscious experience. On the other hand, if consciousness is field-like in nature, perhaps information could be utilized across a small gap, even if interconnections to surrounding tissue were severed (Libet, 1994). Presumably, volitional acts would be limited in range similarly to the incorporation of information. Thus integrative and volitional action of the CMF would be limited by various physical characteristics of the brain, such as the size and nature of the gap which could be crossed. Thus if volition occurs (whether via the CMF or any other means), such characteristics and limitations would be part of the description of its effects, and would be an addition to presently known physical laws.

The Unified Field and Hyperdimensional Space

Hagelin (1987) has proposed that consciousness is the same as the unified field, which consists of all known fields -- electromagnetic, strong, weak, and gravity. The basic nature of consciousness is unknown, and the latter proposal is neither proved nor disproved. However, volition, by its nature, must produce effects which are different from those of presently known fields. Therefore, the unified field, which is identical to the four known fields, cannot account for volition. If it is held that consciousness can affect the physical world, an additional hypothesis must be added, and Hagelin suggests that consciousness acts via collapse of the wave function.

It is now known that many properties of particles and fields can be accounted for in terms of symmetries. (An object is said to have a symmetry if its description remains the same when it is rotated or undergoes some other transformation with respect to some coordinate space.) These symmetries express underlying degrees of freedom of a system, and because of them, particles and fields can be described as residing in hyperdimensional spaces (Pagels, 1985). In order to describe the unification of gravity with the other forces, it must be supposed that space-time itself has ten dimensions (Kaku, 1994). Four of these dimensions are the ones we ordinarily observe (three for space and one for time), and the rest are considered to be curled up into a very small size, but are nonetheless essential for properly describing this unification. In this way, the totality of particles and fields is described by a base space of ten dimensions of space-time and a large number of additional (non-space-time) dimensions which account for the various symmetries of the particles and fields (Kaku, 1994).

The exact nature of this hyperdimensional space is presently unknown, although the various versions of string theory are considered to be the best candidates (Kaku, 1994). However, in quantum mechanics not all physical quantities are simultaneously observable, and the mathematical description of the complete set of all observables which can be simultaneously measured provides an essential starting point in the description of this hyperdimensional space. Furthermore, Sirag (1993, 1996) has pointed out that another space, defined by this set of observables, also plays an important role in describing the total hyperdimensional space. He calls this space an eigenvalue space or a reflection space, and it is a part of all unified field theories.¹⁴ For instance, a well-known unified theory which links the elementary particles is based on a symmetry structure called SU(5), which has a 4-dimensional reflection space called A₄, and a current version of string theory is based on the symmetry structure E₈xE₈, where E₈ refers to an 8-dimensional reflection space (Sirag, 1993).

The relevance of these reflection spaces to consciousness and volition is the following. It can be shown, by means of a mathematical theorem, that a reflection space can be extended to two different hyperdimensional spaces, each with different properties. Thus one can conceive that one of these spaces describes all the symmetry properties of the physical world. However, if one of the spaces describes all of the physical world, the other space must be something different, and Sirag has proposed that the other space corresponds to Universal Mind. Consciousness would then correspond to the intersection of the two larger spaces, i.e., the reflection space which describes observables (Sirag, 1993, 1996).^15,16

¹⁴ Technically, the reflection space has all simultaneous charge-like observables as basis elements. The eigenvalues of these observables, which determine the "charges" (e.g., electric charge, color charge) carried by the particles, specify the vertices of a highly symmetrical figure in the reflection space. Thus each vertex of this figure corresponds to a particle, and particle interactions correspond to the reflections of the vertices into each other. All simple reflection spaces can be classified in terms of the Coxeter types A_n, D_n, E₆, E₇ and E₈ (Sirag, 1993). Manyother important mathematical structures used in unified field theory and string theory can also be classified in terms of these Coxeter types (Sirag, 1996).

¹⁵ One of the spaces is a Lie algebra, and the other, which Sirag calls a McKay group algebra, is based on a finite subgroup of SU(2). Sirag bases his unified field theory on the McKay group algebra, and proposes that the properties of Universal Mind are described by the Lie algebra. The reflection space, which corresponds to consciousness, is the Cartan subalgebra of the Lie algebra and a subalgebra of the center of the McKay group algebra (Sirag, 1993).

¹⁶ We should understand that in this theory consciousness is not identified with the unified field or with any mathematical spaces. Rather, the mathematical spaces involved describe the properties of the physical world, Universal Mind, and consciousness, respectively. Because consciousness would correspond to the intersection of the two larger spaces, it would have some (but not all) properties of the physical world and some (but not all) properties of Universal Mind.
Because the properties of Universal Mind and the physical world are different, Sirag describes the theory as dualism. However, the properties of the reflection space are associated with each point of space-time, so the theory could also be viewed as a form of panpsychism. Sirag (1993)suggests that human consciousness is more complex than the presumably simple consciousness associated with each point in space-time because of the complexity of the brain.

One of the interesting properties of a reflection space is that it is intimately associated with catastrophe structures, a mathematical term which describes the magnification of small changes. In unified field theory, as in any other part of physics, volition must be added as a new element. (Otherwise, as has been said, one has only determinism or quantum randomness.) However, if consciousness is associated with a reflection space, then volition could act as a very small perturbation on physical systems, because the initial small action could be magnified via a catastrophe structure (Sirag, 1993).

Conservation of Energy and Momentum

In the action of free will, a change is made in the physical world which would not otherwise occur (see the definition of free will in the first section). But such an action would involve a change which would not be accounted for by any physical force, and therefore energy would not be conserved. This has long been considered an argument against free will. However, Mohrhoff (1999) has shown, by examination of the fundamental physics concepts involved in conservation of energy that it should not be expected to hold in the case of free will.

His argument can be summarized as follows. Conservation of energy and momentum occur because of deep underlying symmetries in physical laws. The fact that physical laws are the same at any point of space implies that momentum must be conserved, and the fact that physical laws are the same at different times implies that energy must be conserved. (Of course, details of the way the laws act will be different in different times and places. The symmetries consist of the fact that the basic forms of physical laws are the same.) However, in order for the above laws to follow from these symmetries, two additional considerations must hold. First, space-time must be homogeneous and flat, not curved. However, curved space-time is equivalent to gravity, and the effects of gravity can be neglected for the purpose of analyzing volition. Thus, for this purpose, space-time can be considered to be locally flat. And second, it must be possible to describe all forces on particles in terms of a mathematical function called a Lagrangian. Therefore, if volition entails genuine freedom, and its action is not completely prescribed by some mathematical function which depends on physical conditions, then it need not conserve energy or momentum.

We can now use the above finding to extend the definition of free will given earlier. It was originally said that free will is an influence on physical events which corresponds with mental intention and causes a physical change which would not otherwise occur in identical physical circumstances. However, the careful reader may have noted that the latter definition does not mention freedom and could apply to a random or deterministic form of mental influence, as well as volition. To incorporate the notion of freedom the phrase should be added, "with this influence being neither random nor entirely prescribed by mathematical law."

The Incompatibility of Special Relativity with the Concept of the Present Moment

It seems natural to think of free will as acting in the present, with all events classified as to whether they are past, present or future. However, this concept is not compatible with special relativity. We will see that the concept of a universal present moment, in which all observers can agree on which events have already happened and which have not, is not compatible with special relativity. And we will also see that the concept of a present moment which moves along a person's timeline (called a worldline in special relativity) presents major conceptual problems.

To understand these conclusions it is first necessary to know a few basics of special relativity. An event is something that occurs at a particular place and time, and events can be viewed from different inertial frames, i.e., frames of reference which travel at a constant velocity with respect to each other. For instance, a train traveling across the countryside defines one inertial frame and the countryside defines another inertial frame. Special relativity tells us that observers in different inertial frames do not agree on the distance and time duration between two events (although these measurement differences only become large if the two reference frames are moving at nearly the velocity of light with respect to each other). For instance, unstable particles traveling at nearly the speed of light with respect to an observer appear to decay more slowly than they would if they were at rest, because time duration for the observer is longer than time duration in the rest frame of the particle.

All pairs of events have either a time-like separation, in which case a beam of light can be transmitted from the first event to the second, or a space-like separation, in which case the distance between them is too large to permit a beam of light to travel between them in the time allowed. All observers, in all frames of reference, agree on whether two events have a time-like or space-like separation. And if two events have a time-like separation, then all observers can agree as to which event came first. Thus, in the case of the unstable particles, all observers can agree that the unstable particles exist first and the decay products appear later.

We ordinarily think of a choice as being made at a time called the present, with the universe and all persons in it existing in the present and evolving toward a future which is not yet totally determined. But this concept is not compatible with special relativity. Rather, for any events E₁ and E₂ which have a space-like separation, observers in some inertial frames conclude that E₁ occurs before E₂, observers in other inertial frames conclude that E₂ occurs before E₁, and there is always an additional inertial frame in which observers conclude that E₁ and E₂ happen simultaneously. Thus it is not possible for all observers to agree on the order of events which have a space-like separation, and therefore it is not possible for them to agree on which events have already happened and which have not.

We can approach the problem another way by looking for all events which can be considered simultaneous with an arbitrary event, E₁, in the hopes of finding a set of events which would form the moving present. Figure 1 shows events E₁ and E₃, which have a time-like separation, and event E₂, which has a space-like separation from both of them. As noted above, all observers who directly compare E₁ and E₃ conclude that E₁ happens before E₃. But one can always find an observer whose measurements show that E₁ and E₂ are simultaneous, and another observer whose measurements show that E₂ and E₃ are simultaneous. Combining the latter results implies that E₁ and E₃ are simultaneous. Thus our search for a moving present which can be consistently defined across all reference frames leads to the conclusion that in some sense all events coexist.

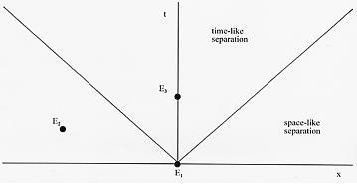
Figure 1

Let us now ask if we can think of an individual person exercising free will, even though the universe cannot evolve as a whole during a "present moment". Any given object never travels faster than light, so all events which happen to that object have a time-like separation. For that reason, all observers can agree on the order of events which occur to an object, and similarly they agree on the order in which a person does things. From this perspective, there would seem to be no problem in claiming that any person has free will and can choose an action out of possibilities offered by his brain programs. All observers agree that the choice, while he stands hesitating, occurs before the result.

Events in the life of any given person form a chain of time-like separations, and one can conceive of a "present moment" moving along this chain of events, called a worldline. Thus one might suppose that a person can act to exert volition in this traveling present moment and thereby change future events in her individual worldline. The problem here comes in trying to account for how the present moment travels along the worldline. We could reasonably begin by supposing that the present moment travels along a person's worldline at a rate which is constant with respect to clocks which are stationary from her point of view, and thereby travels at a constant rate with respect to her physiology. In that case, the present moments of people who stay in the same location will stay in tandem, so that all of them experience the present together. After all, it would be incongruous to suppose that if two people are sitting together having a conversation, one is acting in the present, but for the other the conversation is long past, with his present moment years in the future.¹⁷

¹⁷ Thanks to Avshalom Elitzur for this insight.

But suppose we apply this question of the moving present to the twin paradox, a well known example in special relativity in which one twin stays at home and the other twin travels in a rocket ship for a number of years and then returns to earth. Suppose the rocket ship travels away from earth for 10 years according to earth clocks, and then returns, traveling at 80% of the velocity of light in each part of the trip. Then the twin on earth will have aged 20 years. However, according to clocks on the rocket ship, only 12 years have gone by for the traveling twin (see Davies (1995) for details of this calculation). Suppose, as above, we assume that the present moment travels along each twin's worldline at the same rate as a stationary clock in her

own reference frame, and therefore travels concurrently with her own physiology. For the twin who stayed home, 20 years have passed. We assume that both twins were in the present moment when the traveling twin left, and that the stay-at-home twin is in the present moment when they reunite. By the above rule, the present moment for the traveling twin must also be 20 years later than the date she left earth, as measured by a clock which travels with her. Because only 12 years have passed according to the clock of the traveling twin, her present moment is 20 - 12 = 8 years in the future, when she is again traveling to other stars. The stay-at-home twin is interacting with a zombie-like replica of her sister.¹⁸

Suppose we try to fix this by saying that the present moment must somehow travel such that whenever people meet, they both interact in the present. But a traveler might make many trips and visit many people, with trips from star to star taking a variable amount of time. So that would mean that the rate of travel of the present moment along the traveler's worldline would have to adjust itself to the intended destination, clearly also an incongruous conclusion.

Einstein, whose forte was clearly seeing and embracing the logical conclusions of an idea, concluded that the distinction between past, present, and future is illusory,¹⁹ and stated that a being who understood the lawful action of the universe would "smile about man's illusion that he was acting according to his own free will" (Einstein, 1931). While the possibility that the idea of free will could be reconciled with special relativity cannot be completely ruled out, major difficulties would have to be resolved.²⁰

¹⁸ Conversely, if we assume that the traveling twin is in the present moment when the sisters reunite, then the present moment of the stay-at-home twin has increased by only 12 years, and therefore is 8 years previous to their meeting. In that case the traveling twin is interacting with a zombie-like replica.

¹⁹ Einstein said, "[S]ubjective time with its emphasis on the now has no objective meaning," and "For those of us who are convinced physicists, the distinction between past, present, and future is only an illusion, however persistent." (Einstein and Besso, 1972)

²⁰ The idea of free will is also incompatible with general relativity because in some circumstances a traveler moving around a closed loop in space can return to his starting point at the same time as (or earlier than) when he began (Gribbin, 1992).

The Theory of Universal Time

Is it possible to develop a theory other than special relativity which can account for experimental data, and which would allow all observers to agree on which events are past, present or future? To explore this issue we should pose a fundamental question that Einstein asked when he was developing special relativity. Let us suppose, as Einstein did, that we are not certain whether observers in different inertial frames agree on the times and distances between events and ask how we can determine what these times and distances are for each observer. We will suppose that an Experiment Station is set up, such that any time an observer sends a light signal to the station, it is immediately returned to her. The observer travels at a constant velocity with respect to the station, so she can always calculate the position of the station in terms of her own spatial coordinates and time. She knows when she has sent the signal and when she receives the returned signal. But to make her comparison, she needs to know the time by her clock at which the signal is received at the station. If she knows the velocity of light, she can calculate the time for the signal to travel to the station. Or conversely, if she knows the time by her clock that the signal is received at the station, she can compute the velocity of light. A priori, she doesn't know either, so she has to assume one or the other.

Einstein elected to make an assumption about the velocity of light, and he assumed that it is the same in each inertial frame and independent of the velocity of the source of light. In that case, the time duration for the signal to travel to the station is one half the total time elapsed between sending the signal and receiving the returned one. Einstein made the latter assumption because Maxwell's equations, which describe the laws of electromagnetism, predict that the velocity of light has the same value c in all reference frames. This assumption implies the equations of special relativity.²¹

On the other hand, if we want to suppose that all observers can agree on past, present and future, we can assume that all observers agree on the time the light signal is received at the station, and that is the assumption made by Moon, Spencer, et al. (1989b) in their theory of universal time. One can then follow the implications of this assumption and find what the velocity of light must be. The result is that the velocity of light is always a constant value (c) in the reference frame which is at rest with respect to the source of the light signal. But in all other reference frames it depends on the relative motion of the observer and the source of the light. In our above thought experiment, the observer would consider the velocity of light to be c whenever she sent a signal to the Experiment Station, because in her reference frame the source is at rest. But from her point of view, the velocity of light on the return trip would vary slightly from c, because the return signal originates on the station.

The assumption that the velocity of light is the same in all reference frames has been tested by various experiments, and the experimental data is consistent with this assumption. So if the theory of the universal time is to be viable, its predictions must be sufficiently similar to those of special relativity that they satisfy the same experiments. So far, predictions have been compared for five experiments: the Michelson-Morley experiment, Doppler shifts from binary stars, the Michelson-Gale experiment, the Sagnac experiment, and aberration of light from stars (Moon, 1993; Moon, Spencer, et al., 1989a, 1990, 1991; Spencer and Shama, 1996), and in these experiments predictions of universal time theory have been as close to experimental values as those of special relativity.²²

²¹ For further discussion of the development of special relativity, see Lindley (1993).

²² However, the claim of Spencer and Shama (1996) that their theory fits the data on stellar aberration better than the prediction of special relativity is incorrect. (Their assertion that special relativity predicts no aberration effect is fallacious and does not take into account the fact, cited by them, that in special relativity the wave front of emitted light always must center on the point at which it was emitted. When adjustment is made for this point, special relativity and the theory of universal time make identical predictions for stellar aberration.)

As noted above, Maxwell's equations predict that the velocity of light has the same value c in all reference frames. On the other hand, the theory of universal time makes a different assumption, so in this theory the fundamental laws of electromagnetism have a slightly different form than those described by Maxwell's equations (Moon, Spencer, et al., 1994a, 1994b). The predictions of these revised laws appear to be very similar to those of Maxwell's equations in most practical cases, but Moon, Spencer and co-workers (1989b) are searching for examples in which predictions are sufficiently different that the two sets of laws could be distinguished experimentally.

Because today's physics is highly unified, there is a further issue which any theory that challenges established ideas must address, and that is its compatibility with unified field theory. In modern physics the electromagnetic force is unified with the weak force, and the symmetry properties of the electromagnetic equations form an integral part of this unification (Kaku, 1994). For the theory of universal time to be compatible with unified field theory, the new electromagnetic equations would have to have appropriate symmetry properties. Also, unified field theory is confirmed by experimental data, such as the masses of various particles, and any modifications to its predictions which might result from revised electromagnetic equations would have to be compatible with this data. In this relatively early stage of universal time theory, these ramifications are unknown and it remains to be seen if these requirements can be satisfied.

In summary, in the theory of universal time, all observers can agree on whether any event is past, present or future. The researchers who present this theory have not discussed its relevance to free will. However, because of the latter point, it is compatible with the idea of free will and avoids the major conceptual problems special relativity presents in this regard. The theory of universal time has not so far been ruled out by any experimental considerations. Nevertheless, it is very different from currently accepted ideas in physics, and its ramifications would have to be extensively explored, and checked experimentally, before it could be accepted.

Are We Reaching the End of Physics?

The fundamental physics of the particles involved in ordinary matter, plus all particles created in accelerators, is now considered well understood. The Standard Model says there are twelve fundamental particles -- six quarks, which combine to make protons, neutrons and other particles, and six leptons, which include the electron and neutrino. Similarly, the Standard Model accounts for interactions between the matter particles by means of twelve force particles -- a photon (for electromagnetic interactions), three weakons (for weak interactions), and eight gluons (for the strong force). It is possible that a few surprises could still occur which would change the model somewhat. For instance, if the neutrino should have a non-zero mass, the Standard Model would have to be adjusted to some extent. But this is not expected to change the basic ideas, such as that protons are made up of three quarks.

Gravity has not yet been unified with the other forces, and theories about point particles have had the problem of infinities which have to be subtracted out of calculations. However, string theory, which says that particles are vibrations of strings, appears to have the potential to solve both problems and to be the means by which unification of all the forces can be achieved. In this sense, the fundamental physics underlying all ordinary particles and forces, plus all particles created in accelerators, appears to be nearing completion.

Of course, new sorts of fundamental physics could take place at very high energies, much higher than those achieved in present accelerators. However, the theory which describes the presently known particles and forces predicts that there is a "desert," beginning with energies slightly above those now achieved and ranging to the ultrahigh energies at which the strong force is unified with the electroweak force, in which no new fundamental physics is expected to occur (Pagels, 1985). There is no practical means of building accelerators which can produce energies much beyond the beginning of this desert, let alone to the other side of it.

Some experimental predictions regarding ultrahigh energies can be tested through models of cosmology, because the evolution of the universe shortly after the big bang involved these energies. However, models of cosmology involve many different strands of physics, all incorporated into a single model. So it would be difficult to make a definitive test of any new element of particle physics which would involve these ultrahigh energies. For these reasons it is expected that further advances in fundamental physics will occur only occasionally and, although they may modify our present understanding, will not completely overthrow it. Some physicists are even suggesting that we are coming to the end of fundamental physics (Horgan, 1997; Lindley, 1993). From this perspective, the past century, in which we have seen the development of quantum mechanics, the Standard Model based on symmetry properties, and string theory, appears to be a unique time in physics, with no major principles of any sort remaining to be found.

This does not mean that technological applications of physics would stop. There are undoubtedly many new applications which are not presently even thought of. And this does not imply any slowing of progress in biology or related sciences. As Scott (1995) has emphasized, at the molecular level biological processes are so complex and depend on such an immense number of factors that they must be described phenomenologically at the level of biology. Thus for practical purposes, biological processes can be treated as following independent laws (such as the Hodgkin-Huxley equations described above). These laws presumably trace back to the ordinary dynamic and thermodynamic laws of physics and must be consistent with them. However, the fact that they can be treated as independent means that many new biological discoveries can be made, even if they rest on laws of physics which are completely known.

What does all this say about the possibility of volition? First, we must understand that the recent discussion about the end of physics applies to particle physics, not to consciousness. The latter is at best only a fringe subject within physics, and the term "consciousness" is not even listed in the physics abstracts. The physics of today is about tangible measurable things, not an evanescent thing like consciousness. In this respect none of the above can be taken as an argument against volition. On the other hand, as has been emphasized herein, volition cannot be explained in terms of presently known physical laws, because these encompass only determinism and randomness, and the latter are not what is meant by volition. Thus an addition to physical laws would be needed to describe its effects.

In considering the nature of such an addition, we should note that the act of volition presumably, or plausibly, makes use of information from different parts of the brain. In other words, consciousness can integrate information independently of the brain and then act on the brain using this integrated information. But if consciousness can do this via volition, it is likely, or at least plausible, that it also performs integrative functions which contribute to ordinary brain processing. A number of researchers have proposed that consciousness performs this sort of integrative function independently of the brain (Libet, 1994; Sperry, 1969), and various specific proposals have been made. For instance, Popper and Eccles (1977) propose that this integrative function contributes to vision processing, as does Burns (1991). Popper and Eccles point out that the brain takes different amounts of time to process different sensory modes, and propose that sensory information is adjusted to concurrent times by such a function. Bohm (1982) holds that insight comes about through the action of consciousness. And Penrose (1994) argues that mathematical understanding, and by extension conscious understanding in general, is carried out by such an integrative function.

It is not presently known whether volition and the above integrative action exist. However, we have reviewed various proposals about the way in which the action of consciousness might produce an effect on ordinary matter -- via emergent processes, the ordering of quantum randomness, a new field-like entity (the CMF), or a new set of symmetry properties, different from but related to those of ordinary matter. At the present time such models have primarily focused upon finding gateways for volition, i.e., they set up a framework (such as emergence or ordering of randomness) through which volition might act. However, it seems likely that the action of consciousness on matter would have various characteristics and limitations. Some limitations can be inferred from experimental results in brain research (e.g., in a split brain the information in one hemisphere is not transferred to the other, which suggests that intact connections, or only a small gap in connections, are needed for volition to act). And specific models predict additional limitations which would be particular to the model (e.g., in the wave function collapse hypothesis, the necessity for quantum coherence would seem to limit the action of volition to sub-cellular structures). The differing predictions of different models can serve to some extent as tests of the models.

In summary, the effects of volition cannot be accounted for by presently known physical laws, which involve only determinism and randomness. Yet much of our daily lives, as well as our moral and ethical systems, are based on the assumption that we have free will, and it seems likely that it does in fact exist. Any proposal that volition exists must necessarily involve a radical addition to presently known physical laws. We can expect that this addition would not only state the general sort of gateway (perhaps one of those above) through which consciousness can affect matter, but also principles specifying the physical characteristics and limitations associated with these effects. If volition exists, then physics stands at a new frontier, in which these principles are yet to be discovered.

Acknowledgements

My thanks to David Burrows, Anthony Freeman, Michael Silberstein, and Saul-Paul Sirag for comments on the draft version of this article.

References

Abbott, L.F., and Wise, M.B. (1981), `Dimension of a quantum-mechanical path', American Journal of Physics, 49(1), pp. 37-39.

Bateson, G. (1979), Mind and Nature: A Necessary Unity (New York: Dutton).

Bohm, D. (1982), Wholeness and the Implicate Order (London: Routledge and Kegan Paul).

Bohm, D., and Hiley, B.J. (1993), The Undivided Universe (New York: Routledge).

Burns, J.E. (1990), `Contemporary models of consciousness: Part I', Journal of Mind and Behavior, 11, pp. 153-172.

Burns, J.E. (1991), `Contemporary models of consciousness: Part II', Journal of Mind and Behavior, 12, pp. 407-420.

Burns, J.E. (1996), `The possibility of empirical test of hypotheses about consciousness', in Toward a Science of Consciousness, eds. S.R. Hameroff, A.W. Kaszniak, and A.C. Scott, pp. 739-742 (Cambridge, MA: MIT Press).

Burns, J.E. (1998), `Entropy and vacuum radiation', Foundations of Physics, 28(7), pp. 11911207.

Chalmers, D.J. (1996), The Conscious Mind: In Search of a Fundamental Theory (New York: Oxford University Press).

Crick, F. (1994), The Astonishing Hypothesis: The Scientific Search for the Soul (New York:

C. Scribner's Sons). Davies, P. (1974), The Physics of Time Asymmetry (Berkeley, CA: University of California Press).

Davies, P. (1995), About Time: Einstein's Unfinished Revolution (New York: Simon & Schuster).

Dennett, D.C. (1984), Elbow Room: The Varieties of Free Will Worth Having (Cambridge, MA: MIT Press).

Einstein, A. (1931), `About free will', in The Golden Book of Tagore (Calcutta).

Einstein, A., and Besso, M. (1972), Correspondence 1903-1955 (Paris: Hermann).

Goswami, A. (1993), The Self-Aware Universe (New York: Tarcher/Putnam).

Gribbin, J. (1992), Unveiling the Edge of Time (New York: Harmony Books).

Griffin, D.R. (1998), Unsnarling the World-Knot: Consciousness, Freedom, and the Mind-Body problem (Berkeley, CA: University of California Press). Hagelin, J.S. (1987), `Is consciousness the unified field? A field theorist's perspective', Modern

Science and Vedic Science, 1, pp. 29-87.

Horgan, J. (1997), The End of Science (New York: Broadway Books).

Jammer, M. (1974), The Philosophy of Quantum Mechanics (New York: Wiley).

John, E.R. (1976), `A model of consciousness', in Consciousness and Self-Regulation, Volume 1, eds. G.E. Schwartz and D. Shapiro, pp. 1-50, (New York: Plenum).

Kaku, M. (1994), Hyperspace (New York: Oxford University Press).

Kim, J. (1993), Supervenience and Mind: Selected Philosophical Essays (Cambridge, U.K.:

Cambridge University Press). Libet, B. (1987), in Encyclopedia of Neuroscience, Vol. I, ed. G. Adelman (Birkhauser).

Libet, B. (1994), `A testable field theory of mind-brain interaction', Journal of Consciousness Studies, 1(1), pp. 119-126.

Lindley, D. (1993), The End of Physics: The Myth of a Unified Theory (New York: BasicBooks).

McGinn, C. (1991), The Problem of Consciousness (Oxford: Basil Blackwell).

Mermin, N.D. (1990), `Simple unified form for the major no-hidden-variables theorems', Physical Review Letters, 65(27), pp. 3373-3376.

Mohrhoff, U. (1999), `The physics of interactionism', Journal of Consciousness Studies (in press).

Moon, E.E. (1993), `A postulational formulation of the Michelson-Morley experiment', Physics Essays, 6(4), pp. 487-491.

Moon, P., Spencer, D.E., Mirchandaney, A.S., Shama, U.Y., and Mann, P.J. (1994a), `The electrodynamics of Gauss, Neumann, and Hertz', Physics Essays, 7(1), pp. 28-33.

Moon, P., Spencer, D.E., Mirchandaney, A.S., Shama, U.Y., and Mann, P.J. (1994b), `The force between current elements', Physics Essays, 7(2), pp. 223-232.

Moon, P., Spencer, D.E., and Moon, E.E. (1989a), `Binary stars from three viewpoints', Physics Essays, 2(3), pp. 275-287.

Moon, P., Spencer, D.E., and Moon, E.E. (1989b), `Universal time and the velocity of light', Physics Essays, 2(4), pp. 368-374.

Moon, P., Spencer, D.E., and Moon, E.E. (1990), `The Michelson-Gale experiment and its effect on the postulates on the velocity of light', Physics Essays, 3(4), pp. 421-428.

Moon, P., Spencer, D.E., and Uma, S.Y. (1991), `The Sagnac effect and the postulates on the velocity of light', Physics Essays, 4(2), pp. 249-252.

Pagels, H.R. (1985), Perfect Symmetry (New York: Simon and Schuster).

Penrose, R. (1994), Shadows of the Mind (New York: Oxford University Press).

Petrosky, T., and Rosenberg, M. (1997), `Microscopic non-equilibrium structure and dynamical model of entropy flow', Foundations of Physics, 27(2), pp. 239-259.

Popper, K.R., and Eccles, J.C. (1977), The Self and Its Brain (New York: Springer International).

Prigogine, I. (1980), From Being to Becoming (New York: W.H. Freeman).

Prigogine, I. (1997), `From Poincaré's divergences to quantum mechanics with broken time symmetry', Zeitschrift für Naturforschung, 52a, pp. 37-47.

Scott, A. (1995), Stairway to the Mind (New York: Copernicus).

Seager, W. (1995), `Consciousness, information and panpsychism', Journal of Consciousness Studies, 2(3), pp. 272-288.

Searle, J.R. (1992), The Rediscovery of the Mind (Cambridge, MA: MIT Press).

Silberstein, M. (1998), `Emergence and the mind/body problem', Journal of Consciousness Studies, 5(4), pp. 464-482.

Sirag, S.-P. (1993), `Consciousness: A hyperspace view', appendix to Roots of Consciousness, 2nd Edition, by J. Mishlove, pp. 327-365 (Tulsa, OK: Council Oak Books).

Sirag, S.-P. (1996), `A mathematical strategy for a theory of consciousness', in Toward a Science of Consciousness, eds. S.R. Hameroff, A.W. Kaszniak, and A.C. Scott, pp. 579-588 (Cambridge, MA: MIT Press).

Spencer, D.E., and Shama, U.Y. (1996), `Stellar aberration and the postulates on the velocity of light', Physics Essays, 9(3), pp. 476-483.

Sperry, R.W. (1969), `A modified concept of consciousness', Psychological Review, 76, pp. 532-536.

Sperry, R.W. (1977), `Forebrain commissurotomy and conscious awareness', Journal of Medicine and Philosophy, 2, pp. 101-126.

Sperry, R.W. (1983), Science and Moral Priority (New York: Columbia University Press).

Stapp, H.P. (1996), `The hard problem: A quantum approach', Journal of Consciousness Studies, 3(3), pp. 194-210.

Walker, E.H. (1975), `Foundations of paraphysical and parapsychological phenomena', in Quantum Physics and Parapsychology, ed. L. Oteri, pp. 1-53 (New York: Parapsychology Foundation).

Wick, D. (1995), The Infamous Boundary (New York: Springer-Verlag).

Wilson, D.L. (1999), `Mind-brain interaction and violation of physical laws', Journal of Consciousness Studies (in press).

Zeh, H.-D. (1989), The Physical Basis of the Direction of Time (New York: Springer-Verlag).

Zurek, W.H., and Paz, J.P. (1994), `Decoherence, chaos, and the second law', Physical Review Letters, 72(16), pp. 2508-2511.