1. The Traditional Mind-Body Problem
The traditional mind-body problem is ontological. It addresses the
fundamental nature of the conscious and cognitive mind and the relationship
between mental and physical events. Arguably, it is this ontological focus
that has kept the problem open even after more than one century of
groundbreaking work in the behavioral and brain sciences. These sciences
have already discovered physical events correlated empirically with specific
mental events. But the further claim that all mental events are numerically
identical to physical events remains controversial. Doubters can still insist
that this increase in empirical knowledge has not produced any philosophical
advance over historical materialisms (ones formulated prior to this increase
in empirical knowledge).
Consider one example. Neuropsychologists have discovered that the
capacity of primates (humans included) to recall and act upon explicit
memories of previous episodes depends upon activity in subcortical
structures in the brain’s medial temporal region (especially the
hippocampus and hippocampal formation). Empirical evidence includes both
clinical and experimental documentation that bilateral damage to these
structures severely impairs performance on tasks requiring subjects to use
this type of memory (Kandel and Squire, 1999). (In humans, bilateral
damage to these structures produces a pathological syndrome called global
amnesia. See Kolb and Whishaw, 1996.) But one can still insist that it
remains as mysterious as ever to identify the experienced episodic memory
with electrochemical activity in these neural regions, or even to claim that
this activity is a component or part of the mental event. What does
knowledge about the location of correlated neural activity, or even details
about the underlying cellular and molecular events, contribute toward
reducing the perennial mystery? (This intuition, expressed using different
arguments and focusing on different features of conscious mental events,
motivates the much-discussed recent criticisms of physicalism by Thomas
Nagel 1974, 1989, Jackson 1983, and Chalmers 1996.) Philosophy of mind
remains to this day the battleground over which two ontological intuitions
clash, seemingly without hope of rational resolution:
- That the nature and core properties of mental phenomena as ordinarily
conceived and experienced assures that they cannot be identical to
physical (i.e., neural) events;
- That the domain of the mental should ultimately be brought under the
scope of our otherwise comprehensive and wholly physical scientific
world-view.
2. A Contemporary Perspective
As a way to break this deadlock, it has been fashionable for nearly
four decades to construe intuition 1 as resting on allegiance to a primitive
theory—"folk" or "common sense" psychology—deeply ingrained in existing
human cultures. The central posits of this theory, beliefs and desires, are
said to be theoretical expressions, constructed to explain and predict
behavior. The "ontological facts about the mental," paraded as
"conceptually autonomous" by defenders of intuition 1, depend upon
constitutive principles and generalizations of this theory. Some find this
construal exciting because it can ground an eliminativist account of the
mind. Future scientific research and theory might reveal the scientific
impropriety of folk-psychological principles and generalizations, as past
science did with folk theories of witchcraft and proto-scientific theories
about caloric fluid. If this happens, eliminativists conclude that the mind as
ordinarily conceived and experienced does not exist, in the same way that
witches and caloric fluid doesn’t exist (Feyerabend 1963; Rorty 1970, Paul
Churchland 1981, 1989; Patricia Churchland 1986). But one need not be an
eliminativist to find value in this "folk theory" construal of intuition 1. This
construal also allows us to reformulate the traditional mind-body problem as
first and foremost a question about intertheoretic relationships, and only
secondarily as an ontological question. Our justified ontological conclusions
about the fundamental nature of the mind (as ordinarily conceived and
experienced) will depend upon whether the appropriate intertheoretic
relationship(s) obtain between folk psychology and its scientific successors
(scientific psychology, neuroscience). Historically in science, intertheoretic
reduction has been a relation thought to yield cross-theoretic ontological
conclusions about the entities and properties of the reduced theory. For
obvious reasons, I’ll call the resulting approach the Intertheoretic Relation
(IR) Reformulation of the mind-body problem. Its guiding hope is that by
reorienting the traditional issue away from its ontological focus, and making
the ontological conclusion justified by—secondary to and dependent
upon—the methodologically prior intertheoretic reduction issue, the deadlock
that surrounds the traditional problem might be overcome: in a way that
brings to bear some of the rich and rigorous resources of 20th century
philosophy of science and contemporary cognitive and brain science upon
this perennial philosophical issue.
3. The IR Reformulation is Born Following Ernest Nagel’s (1961)
Theory of Intertheoretic Reduction
The early identity theories of U.T. Place (1956) and J.J.C. Smart
(1959) did not utilize any account of intertheoretic reduction. But after
Ernest Nagel’s (1961) work filtered beyond the philosophy of science, his
account—especially his "temperature-to-mean molecular kinetic energy"
example—became a common physicalist resource. It became so common
that Fodor (1974) took himself to be attacking the entire reductionist
program in philosophy of mind by pointing out difficulties that the "special
sciences" pose for Nagel’s account. In footnote 2 Fodor asserted (without
argument) that "many of the liberalized versions of reductionism suffer from
the same base defect as what I shall take to be the classic form of the
doctrine." (The "classic" form was built on Nagel’s account, published
thirteen years prior to Fodor’s essay. Some works become classics very
quickly!)
In the spirit of logical empiricism, Nagel held that the reduction of one
theory to another consists of a logical derivation of the laws or principles of
the former (the reduced theory TR) from the laws or principles of the latter
(the reducing or basic theory TB). In interesting cases, where TB’s
descriptive vocabulary lacks terms from that of TR ("heterogeneous" cases,
as Nagel 1961 called them), various "correspondence rules" or "bridge
principles" must be introduced to effect the derivation. Eschewing niceties
and many details, we can represent Nagel’s account as follows:
TB & BP (as necessary)
logically entails
TR.
BP stands for whatever bridge principles are necessary to connect up
disparate elements of TR’s with TB’s vocabulary. Also in the spirit of logical
empiricism, Nagel characterized TR, TB, and BP syntactically, as sets of
statements or propositions.
The traditional mind-body problem focuses on the ontological status of
mental properties, states, and events as ordinarily conceived and
experienced. Reformulated in light of the "theory" status of folk psychology
(as the theory with which our common sense mentalistic ontology is
affiliated) and Nagel’s theory of intertheoretic reduction, the issue
becomes: Will future cognitive and brain science develop theories (TB’s)
from which, with appropriate BPs, the generalizations of folk psychology
(TR) are derivable? If physicalism about the (common sense) mental is to
be defended in light of this reformulation, some theory from the physical
sciences must occur at the end of a chain of reductions: from folk
psychology to . . . to, e.g., neuroscience. And each link in this chain must
meet the demands that Nagel’s account places on the intertheoretic
reduction relation.
What does the IR reformulation accomplish? What do we achieve by
reformulating the traditional issue in this fashion? First, it replaces the murky
notion of "ontological reduction" with a well-studied, (circa early-1960
philosophy of science), scientifically-grounded notion: intertheoretic
reduction. It allows proponents to appeal to cases from the history of
science to defend future psychology-to-physical science reductions. Taking
intertheoretic reduction as the central issue provides clear and defensible
verdicts about the variety of philosophical arguments brought to bear on the
traditional mind-body problem. Evidence and arguments relevant to deciding
for or against predicted future psychology-to-physical science theory
reductions are legitimate; evidence and arguments irrelevant to this issue
are not. One interesting consequence of this methodological prescription is
that the familiar philosophical tactic of "conceptual separability" thought
experiments often used to "prove" non-identity—our capacity to imagine the
one property or event occurring in the absence of the other—is irrelevant.
There are plenty of properties and events affiliated via the bridge principles
in intertheoretic reductions that can be "conceptually separated": lightning
and large-scale atmospheric electron discharge, for example. Nevertheless
the identities in these cases have been established on clear scientific
grounds. Yet consider the number of recent anti-physicalist arguments that
rest upon the "logical possibility" of e.g., conscious minds in physical
vacuums or unconscious zombies with functioning human nervous systems.
If the IR reformulation captures the traditional mind-body problem, this
popular tactic is irrelevant. The underlying arguments are invalid: conceptual
separability does not imply theoretic irreducibility, from which
cross-theoretic identities can follow. The methodological upshot is
significant: we can finally address questions about the ontology of mind
from the perspective of a rigorous philosophy of science.
4. The Revolt Against Nagel
As philosophers of mind began applying Nagel’s account to the
mind-body problem, the account itself came under decisive attack within the
philosophy of science. Constructed within the logical empiricist program,
Nagel’s account incorporated that program’s strengths and weaknesses
qua theory of science. One weakness, stressed increasingly throughout the
1960s, was its assumption about the continuity of scientific progress.
Reduction as deduction of TR from TB reflects this assumption. Modus
tollens and logical consistency both require that if some principles of TR are
false, then something in the reducing complex must be, also. But this
consequent contradicts the assumed truth of TB and the BPs. Careful
historical analysis revealed that principles of the TR in some "textbook"
scientific reductions are false. Falling bodies near the surface of the earth
do not really exhibit uniform vertical acceleration over any finite interval. Yet
this assumed uniformity is central to Galilean physics. Galilean physics is
empirically false. It does not describe correctly the behavior of falling
objects in any portion of the actual world. Yet the reduction of Galilean
physics to Newtonian mechanics is a "textbook" historical case of the
relation.
For many historical examples (including the one just discussed),
Nagel’s account can handle falsity in the principles of TR with a simple
addition to the premises of the derivation. These must include not only the
principles of TB and the appropriate BPs, but also various and often
counterfactual boundary conditions or limiting assumptions (BC/LA) on the
applicability of TB. In the Galilean physics-to-Newtonian mechanics case,
we can conjoin with the Newtonian principles either a counterfactual
assumption describing conditions near the surface of the earth that permit
uniform vertical accelerations over a finite interval, or a counterfactual
assumption that limits the applicability of Newton’s laws to moving bodies
that fall distances only negligibly greater than zero. From this reducing
complex the principles of Galilean physics (TR) can be derived, and their
falsity is explained by and hence confined to the counterfactual BC/LA
component.
Yet this strategy cannot handle every historically-acknowledged
reduction of a false TR. Sometimes a TR turns out to be so "radically" false
that central elements of its ontology must be rejected as illusory or
completely uninstantiated. This creates a problem for the status of the BPs.
Referents of the descriptive terms of TB cannot be identical to nor
nomologically connected with the "referents" of descriptive terms of TR if
the latter are non-existent or nowhere instantiated. And some central posits
of "textbook" TRs appear to meet this condition. Relativistic mass is a
two-place relation between an object and countless reference frames.
Classical mass is a one-place property of objects. A two-place relation can
never be identical to a one-place property, Relativistic mass is never even
co-extensive with classical mass at any actual velocity. Strictly speaking,
classical mass is nowhere instantiated in physical reality: no physical object
actually has that property. So what is the logical status of a BP that
"bridges" these elements of the disparate theoretical vocabularies:
especially if we construe BPs as laws? Neither synonymy nor material
identity between the terms’ extensions are plausible interpretations. And
no BC/LA appears to alleviate this "radical" falsity within the TR.
Close historical investigations into actual scientific practice and results
revealed a number of intertheoretic reductions that implied significant
corrections to the TR. Even the case that Nagel (1961) used to illustrate his
approach turned out to involve a significantly false TR: classical equilibrium
thermodynamics-to-statistical mechanics and microphysics. This case is a
limit reduction, and the limits in which the laws of equilibrium
thermodynamics can be derived from statistical mechanics are never
actually realized (e.g., an infinite number of gas particles whose diameter
divided by the average distance between particles is only negligibly greater
than zero). At best, equilibrium thermodynamical explanations approximate
the actual microphysical events and their statistical distributions. Second,
many key thermodynamical concepts fragment into distinct statistical
mechanical/microphysical concepts, with each of the latter being the
appropriate candidate for "identification" within the appropriate limit.
(Clifford Hooker 1981 demonstrates this point for "entropy.") Third, a
diachronic view of this case reveals mutual developmental feedback
between the TR and TB. Problems confronting classical thermodynamics
(TR) spurred the application and development of statistical approaches.
And the injection of statistical results and developments (TB) back into
classical thermodynamics yielded corrections to the latter resulting in more
accurate predictions. (Hooker 1981 provides a nice introduction to these
details. Bickle 1998, chapters 2 and 3, shows how to capture some of
these details within a quasi-formal account of the intertheoretic reduction
relation, discussed further in section 7 below.)
What consequences do these features have for the ontology of
classical thermodynamics? Hooker (1981) is explicit on this point: "In a fairly
strong sense thermodynamics is simply conceptually and empirically wrong
and must be replaced" (p. 49). This quote reflects one important criticism
against Nagel’s account. Intertheoretic reductions in actual science
typically imply significant corrections to the TRs. Beyond a point, these
corrections make logical empiricist proposals for handling falsity within the
TRs increasingly untenable.
Criticisms like this one spurred a variety of alternative approaches to
reduction. Patrick Suppes (1956, 1965) proposed characterizing scientific
theories semantically, in terms of a set of models sharing some
set-theoretic structure. He in turn characterized intertheoretic reduction as
set-theoretic isomorphism (the formal analog of "sameness of structure").
He applied his account explicitly to psycho-physiological reduction: "The
thesis that psychology may be reduced to physiology would be for many
people appropriately established if one could show that for any model of a
psychological theory it was possible to construct an isomorphic model within
physiological theory" (1965, p. 59). His account turned out to be too weak,
however. Kenneth Schaffner (1967) pointed out that "different and
nonreducible (at least to one another) physical theories can have the same
formal structure—e.g., the theories of heat and hydrodynamics—and yet we
would not want to claim that any reduction could be constructed here" (p.
145). In other words, Suppes’ account implied that obvious cases of
non-reducibility meet the conditions on an intertheoretic reduction. So
set-theoretic isomorphism is too weak: its obtainment is not sufficient for
intertheoretic reduction.
Another alternative that received more attention is often attributed
independently to Karl Popper (1962), Paul Feyerabend (1962), and Thomas
Kuhn (1962). This approach focused on the difficulties that obtain in trying to
characterize a "close fit" between a TR and "special cases" of the TB (i.e.,
those cases already cordoned off from TB proper by application of
counterfactual BC/LAs). Its central contention held that in addition to
explaining why the TR works in situations where it does, the TB must also
explain why the TR fails in other expected applications. In this sense,
successful reductions correct the TRs. Feyerabend (1962) famously
expressed this contention by denying that reductions involve deductions at
all. Instead, he insisted that "ontological replacement" was the key to
understanding the relationship between a TR and its "incommensurable" TB.
He went so far as to call for philosophers of science to abandon the search
for any formal or "objective" account of intertheoretic reduction or scientific
progress.
Like Suppes, Feyerabend also applied his approach explicitly to the
"mind-body problem":
In the course of the progress of knowledge, we may have to
abandon a certain point of view and the meanings connected with
it—for example, if we are prepared to admit that the mental
connotations of mental terms may be spurious and in need of
replacement by a physical connotation according to which mental
events, such as pain, states of awareness, and thoughts, are
complex physical states of either the brain or the central nervous
system, or perhaps the whole organism. (1962, pg. 30)
He advocated this view (albeit cautiously at first) for "all so-called mental
states." Using the resources of his approach to reduction, the philosopher of
mind’s agenda is to "develop a materialistic theory of human beings." Such
a result would "force us to abandon the mental connotations of the mental
terms, and we shall have to replace them with physical connotations" (1962,
p. 90). Within a reformulation of the traditional mind-body problem built on
Feyerabend’s approach to reduction, eliminative materialism received it
first serious expression and defense.
Eliminative materialism remains deeply controversial. Its current status
makes it enlightening to look back at the writings of some famous "identity
theorists" throughout the mid-1960s, as their views came under attack.
Feyerabend’s eliminativism and his "radical empiricist" philosophy of
science that undergirded it began to look increasingly attractive. Just four
years after his influential (1959) paper, for example, J.J.C. Smart claimed
to be
attracted to P.K. Feyerabend’s contention that in defending
materialism we do not need to show its consistency with ordinary
language, any more than in defending the general theory of
relativity we need to show its consistency with Newtonian theory. .
. . Feyerabend is perhaps therefore right in arguing that the
scientific concept of pain does not need to be (and indeed should
not be) even extensionally equivalent with ordinary language.
(1963, p. 660)
Four more years later, Smart clarified his (cautious) change in view. He
admitted to being even closer to Feyerabend, both in philosophical
methodology and eliminativist conclusion, in an attempt to stave off an
"ordinary language" criticism of his earlier "topic-neutral translation"
approach to mental terms:
I am even doubtful now whether it is necessary to give a
physicalist analysis of sensation reports. Paul Feyerabend may be
right in his contention that common sense is inevitably dualistic,
and that common sense introspective reports are couched in a
framework of a dualistic conceptual scheme. . . . In view of
Bradley’s criticisms of my translational form of the identity thesis,
I suspect that I shall have to go over to a more Feyerabendian
position. (1967, p. 91)
Nor was Smart the only famous identity theorist attracted to Feyerabend’s
resources and results. In his (1967) postscript, Herbert Feigl also moved
explicitly toward Feyerabend’s views: "I now agree with Smart (and
perhaps with Feyerabend) that within the conceptual frame of theoretical
natural science genuinely phenomenal (raw feel) terms have no place" (p.
141). He cited a scientific analogy that later became prevalent in
eliminativist writings: the properties of common sense physical objects
vis-à-vis their "successor concepts" from physical science. He concluded
that "the phenomenal predicates used in the description of after-images,
sensations, feelings, emotions, moods, etc., are to be replaced by the (as
yet only sketchily known) neurophysiological and ultimately microphysical
characterizations" (1967, pp. 141-142). (However, Feigl 1967 shied away
from some of the radical consequences of these views that Feyerabend
embraced, appealing to some of Wilfrid Sellars’ ideas in an attempt to
soften them.)
In light of the themes I am developing here, these shifts toward
Feyerabend’s philosophy of science and eliminativist conclusions by early
identity theorists are important for at least two reasons. First, they
demonstrate how intractably dualistic is our common sense ("folk")
conception of the mental. It is not just extremely difficult to find some kind of
physical "translation" for mental terms (even via a "topic neutral"
intermediary): it is probably impossible. Second, these capitulations to
Feyerabend show how attractive philosophers of mind found resources from
the philosophy of science. Every account of intertheoretic reduction that
was taken seriously by philosophers of science was adopted quickly and
explicitly by philosophers of mind in an attempt to reformulate the traditional
mind-body problem.
And so the IR reformulation developed on the back of accounts of
intertheoretic reduction. "Ontological reduction" and "linguistic analysis" gave
way to potentially clearer (and increasingly clarified) notions of intertheoretic
reduction. For many, philosophy of mind became a specialized part of
applied philosophy of science—the philosophy of the cognitive and brain
sciences and their cross-theoretic relations—albeit a part with special
intrigue, since we are its subject matter.
5. Nagel’s Insights Revived and Modified: Schaffner and Hooker
Attractive as some early identity theorists found Feyerabend’s
approach, most Anglo-American philosophers of science were less
enamored by it. Consensus held that his views were too radical, too
dismissive of precise, formal resources to illuminate scientific concepts and
historical episodes. (As radical a critic of orthodox logical empiricism as
Thomas Kuhn 1962 maintained that the majority of scientists spent the
majority of their careers doing "normal science," i.e., puzzle-solving within
an accepted paradigm). Even cases of wholesale theory change—physical
optics-to-electromagnetism, classical thermodynamics-to-statistical
mechanics and microphysics, Newtonian mechanics-to-special relativity
theory—seem to approximate the formal relations proposed by Nagel and
other logical empiricists. Feyerabend dismissed the possibility of accounting
for this sense of "approximation," but many philosophers of science
proceeded on the assumption that something like it could be clarified. What
resulted were accounts of intertheoretic reduction that incorporated
weakened Nagelian conditions, in an attempt to capture features of
scientific history and practice emphasized by Feyerabend and other radical
empiricists.
Kenneth Schaffner’s (1967) General Reduction Paradigm, later
developed more fully and renamed the General Reduction-Replacement
(GRR) model (Schaffner 1992), was the first important attempt explicitly to
conciliate Nagelian conditions with radical empiricist historical insights.
Schaffner’s model included conditions of connectability and derivability that
yielded Nagel’s exact conditions as special cases. But it included
"corrected" reducing and reduced theories (TB* and TR*, respectively) that
weakened these general conditions. Connectability and derivability between
TB* and TR* permitted these relations to hold in cases where (actual) TB
corrects (actual) TR by making more accurate predictions in TR’s domain of
application (at least potentially). (See Schaffner 1992, p. 321, for the
detailed conditions.) Furthermore, TB (or TB*) explains TR in that TR and
TR* stand in a relation of "strong analogy." Hence since TR* is derivable
from TB (or TB*), this being Schaffner’s weakened condition of derivability,
the latter indicates why TR "worked as well as it did historically" or explains
TR’s domain "even when TR is replaced" (Schaffner 1992, p. 321). These
weakened notions "allow the "continuum" ranging from reduction as
subsumption to reduction as explanation of the experimental domain of the
replaced theory" (Schaffner 1992, p. 320). Cases that closely approximate
Nagel’s conditions coalease around the first pole; cases with features
emphasized by the radical empiricists coalease around the second. Both
orthodox logical and radical empiricist intuitions were thereby
accommodated within Schaffner’s GRR model. (Although it must be noted
explicitly that Schaffner has yet to explicate the relation of "strong analogy"
between corrected TR* and actual TR.)
Schaffner offers a further reason in support of his GRR model: the
same one we saw emphasized in the previous section. He writes: "The
flexibility of the GRR model is particularly useful in connection with
discussions concerning current theories that may explain "mental"
phenomena" (1992, p. 320). The IR reformulation lives on! Schaffner
showed in detail how his model applies to a case of (potential) reduction in
psychology and neurobiology: the neural mechanisms of short-term and
long-term learning as revealed by cellular studies in the sea slug, Aplysia
californica (1992, p. 323-329; Bickle 1998, chapter 5, discusses related
features of this same example). Although the cellular and molecular
explanations Schaffner discusses are now somewhat dated (see, e.g.,
Kandel and Squire 1999 for a good introduction to the current account), the
lessons he stressed from this extended discussion remain topical.
According to Schaffner (1992)
This case does not involve laws akin to those in "textbook" cases of
reduction from physics (p. 329).
The reducing complex is an intricate system of causal generalizations
with a variety of scopes of applicability (from nervous systems in
general to specific types of neural processes). These generalizations
are not framed within the vocabulary of a specific science (e.g.,
biochemistry), but rather are characteristically interlevel (e.g.,
containing terms from biochemistry, molecular biology, cellular
neurophysiology, neuroanatomy, and behavioral psychology) (p. 330).
When a phenomenon described at one level (e.g., the behavioral, as
"sensitization") gets explained in lower-level terms (e.g., molecular
mechanisms), the former description is mapped into the lower-level
vocabulary (pp. 330-331).
It is by virtue of this last feature that Schaffner’s GRR generalization of
Nagel’s conditions of connectability and (in light of expected developments
in biochemistry, i.e., the development of some "corrected" TB*) derivability
obtain. The point relevant to my concerns is that Schaffner’s GRR model
appears supple enough to handle the special complexities and details that
psychology-to-neurobiology reductions generate, yet it retains
Nagelian-inspired conditions of connectability and derivability. And it
achieves this concilience using a case that emphasizes actual scientific
details, far beyond the extent that is typical in philosophy of science or
mind.
Clifford Hooker (1981) provides another approach that amounts (in
part) to a weakened set of Nagel-inspired conditions. Hooker agrees that
intertheoretic reduction involves deduction, with TB and possibly
counterfactual BC/LAs serving as premises. But unlike Nagel, the
conclusion of the derivation is not TR; and unlike Schaffner, it is not a
corrected TR* of TR. Instead, what gets deduced is an equipotent
isomorphic image IB of TR, specified within the conceptual framework and
vocabulary of TB. The generalizations comprising IB match the syntactic
structure of those comprising TR and provide explanations (using the
resources of TB) of TR’s domain of application. Simplifying, and ignoring some
complexities, we can express Hooker’s account as follows:
TB & BC/LA (as needed)
logically entails
IB (a set of theorems of [restricted] TB)
e.g., (x)(Ax 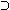 Bx), (x)((Bx & Cx) Bx), (x)((Bx & Cx) 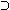 Dx) Dx)
which is relevantly isomorphic to ("analogous to")
TR
e.g., (x)(Jx 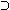 Kx), (x)((Kx & Lx) Kx), (x)((Kx & Lx) 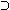 Mx) Mx)
(I adopt this schema from Paul Churchland 1985. The example is meant
only to be illustrative of the "analog relation" between IB and TR. It is not
intended to ground an analysis of the relation (which, incidentally, neither
Hooker nor Churchland ever provides).) It is important not to confuse
Hookewr’s deduced structure IB with Schaffner’s TR*. Hooker’s IB is
characterized completely within the framework and vocabulary of TB;
Schaffner’s TR* is a corrected version of TR. This difference yields the
very different ways that Hooker and Schaffner attempt to capture radical
empiricist insights within a modified Nagelian account, and every topic
discussed in the remainder of this section hinges on this difference. (For this
reason, I’ve changed the symbol Hooker 1981 uses to denote the "analog
structure.")
Hooker acknowledged explicitly the radical empiricist insights about
scientific history and progress built into his approach. But his guiding
intuition is Nagelian:
While the construction of IB within TB might be a complicated
affair—[BC/LA] might be fearfully complex (cf. biological
reductions), counterfactual (e.g., assume continuity), necessarily
counterfactual qua realization (e.g., "force free"), and so on—the
ultimate relation between TB and IB remains straightforward
deduction. (1981, p. 49)
Even his justification of this feature is Nagelian: "TB continues to directly
explain IB and this is the basis for TB’s indirect explanation of TR’s erstwhile
scientific role" (1981, p. 49). Hooker’s guiding idea is that deduction is
necessary for explanatory unity, which remains one goal of his approach to
reduction: a goal he shares with logical empiricists.
Notice that the premises of the deductive component of a Hooker
reduction do not contain bridge principles (BP), unlike either Nagel’s or
Schaffner’s approach. None are needed to effect the derivation. IB is
already specified within (a restricted portion of) TB. There are no disparate
vocabularies to bridge across premises and conclusion. Structures
analogous in some ways to BPs appear in the second stage of the
reduction, involving IB and TR. But these components are only ordered pairs
of terms that indicate the substitutions in IB that yield the actual
generalizations of TR. By themselves, these ordered pairs imply neither
synonymy, material identity, nor coextension. Thus one central difficulty with
Nagel’s approach vanishes: that of specifying the logical status of BPs in
reductions implying significant falsification to the TRs.
Earlier in this section we saw that Schaffner’s (1992) generalizations
of Nagel’s conditions of connectability and derivability yielded a spectrum
of reductions, ranging from ones in which Nagel’s actual conditions are
closely approximated to others displaying features emphasized by radical
empiricists. Hooker’s approach yields a similar spectrum, ranging from
"relatively smooth" to "extremely bumpy" intertheoretic reductions. A
case’s location depends upon the "amount of correction" implied to the TR,
the "closeness of fit" obtaining between the IB and TR. Cases approximating
Nagel’s relation fall near the "smooth" endpoint. The derived IB is
equipotent and strongly analogous in structure to the TR, and few
counterfactual BC/LAs are needed to derive it from the TB. (Historically, the
physical optics-to-electromagnetism reduction seems to reflect these
conditions.) Cases involving features emphasized by radical empiricists fall
toward the bumpy endpoint. Only an IB weakly analogous to TR can be
derived from TB, and this only with the help of numerous and wildly
counterfactual BC/LAs. (Historically, the phlogiston theory-to-oxidative
chemistry case seems to reflect these conditions.) "Mixed" cases sharing
some features of both extremes fall on the spectrum separating these two
endpoints, depending on the "amount of correction" implied to the TR
(captured in these two conditions, the strength of analogy between IB and
TR and the number and counterfactual nature of the BC/LAs necessary to
derive such an IB). (Problematic historical cases for logical empiricism, like
the classical thermodynamics-to-statistical mechanics and microphysics
reduction, seem to reflect these conditions.) However, it is crucial to realize
that according to Hooker’s account, the TR itself is never deduced, not
even in the "smoothest" cases. Rather, it is always the target of a kind of
complex mimicry.
If Hooker’s account of reduction nowhere employs BPs, how does it
justify the cross-theoretic ontological consequences typically thought to
follow from an intertheoretic reduction? Such consequences are justified by
a higher-order relational feature of the intertheoretic reduction. Not only do
historical intertheoretic reductions line up on a spectrum (just described):
the cross-theoretic ontological consequences drawn in specific cases do,
also. The latter range from entity and property/event identities (visible light
is electromagnetic radiation with wavelength between 350-750h m) to
significant conceptual revision (pressure p and temperature T of a gas are
only identical to statistical mechanical/microphysical constructs in an
empirically unrealizable mathematical limit) to outright elimination (there is
no such thing as phlogiston). When we lay out the location of historical
reductions on these two spectra—the intertheoretic reduction "amount of
correction" spectrum and the ontological consequences spectrum—we
discover a rough isomorphism. A case’s location on the intertheoretic
reduction spectrum correlates closely with its location on the ontological
consequences spectrum (see the diagram in Bickle 1998, p. 30). This
observation suggests a strategy for predicting the ontological consequences
of a developing or potential intertheoretic reduction. First discover where on
the intertheoretic reduction spectrum the case appears to be headed (in
terms of "amount of correction" to TR). How equipotent and structurally
analogous is an image IB of TR derivable within TB? How numerous and
wildly counterfactual are the BC/LAs needed to effect the derivation? Which
historical reduction does the case seem most closely to resemble in these
respects? Answers will locate the developing or potential case on
Hooker’s intertheoretic reduction spectrum. The predicted ontological
consequences will then be those obtaining at the roughly isomorphic location
on the other spectrum. The isomorphism across the two spectra that
permits this approach are, as emphasized above, inspired by cases from
the history of science.
We can now see how Hooker’s theory of reduction leads further
support to the IR reformulation of the traditional mind-body problem. It
generates another argument in favor of this approach: the "everything in its
place" argument (Bickle 1998, chapter 2). All the influential "solutions" to the
traditional problem emerge as specific predictions about the future
intertheoretic reducibility (or lack thereof) of folk psychology to proposed
scientific successors. As we saw above, the traditional mind-body problem
is about the ontological status of mental states and events as ordinarily
conceived and experienced. This ontology is commonly assumed to be the
one affiliated with folk psychology qua explanatory theory of cognition and
behavior. Substance dualism thus becomes the prediction that folk
psychology will not reduce completely to any physical science (although it
might reduce completely to some future science of nonphysical substances
and their properties). We remain committed to the entities and properties
postulated by our best explanatory theories. Property/event dualism
becomes the prediction that the ultimate reducing theory for folk psychology
will still postulate special nonphysical (emergent?) properties (essential
subjectivity, intrinsic intentionality, qualia): perhaps ones that obtain only in
complex collections of physical entities. Behaviorism becomes the (unlikely)
prediction that the best future scientific psychology will be some
autonomous behaviorist account, to which folk psychology will smoothly
reduce. This result will yield identities between specific mental states and
specific behavioral dispositions. Functionalism (aka cognitivism, classical
computationalism) becomes the prediction that the best future science of
mind will be some cognitivist/computationalist theory, autonomous from the
physical sciences, to which folk psychology will smoothly reduce. This result
will yield identities between specific mental states and specific nodes in a
processing network mediating between perceptual inputs, other "internal"
processing states, and behavioral outputs. The mind-brain identity theory
becomes the prediction that folk psychology will smoothly reduce to some
future neuroscience (perhaps by way of reducing first to some scientific
psychology that in turn reduces to the neuroscience). This result will yield
identities between specific mental states and specific brain states, events,
and processes. Finally, eliminativism becomes the prediction that folk
psychology will only reduce in bumpy fashion to whatever future scientific
theory best explains human cognition and behavior; eliminative materialism
in particular predicts that neuroscience will provide the best theory and an
ultimately bumpy reducer for folk psychology. The result will be an
elimination of mental states and events as ordinarily conceived an
experienced from our best scientific ontology.
Two additional observations dovetail with this argument. First, this
"everything in its place" argument answers the question as to why so few
influential solutions to the traditional mind-body problem have emerged
(Searle 1985). The above solutions, reformulated as predictions about
possible future intertheoretic reductions, by and large exhaust the sciences
that have been investigated seriously to develop a comprehensive
explanation of human cognition and behavior. Second, the spaces between
the "smooth" and "bumpy" endpoints on the intertheoretic reduction
spectrum and the "retention" and "replacement" endpoints on the ontological
consequences spectrum provide for the possibility of a "revisionary"
outcome for folk psychology (Bickle 1998, chapter 6). There are a variety of
historical cases useful as models for a revisionary psychophysical reduction,
e.g., classical thermodynamics-to-statistical mechanics and microphysics
and classical mechanics-to-general relativity theory. Ontologically speaking,
revisionary physicalism predicts enough conceptual change to rule out
cross-theoretic identities between folk psychology’s propositional attitudes,
developing neurophysiological posits, and their theoretically central
properties. It differs in this fashion from reformulated identity theory.
However, it also denies that folk psychological kinds will undergo the radical
elimination that befell, e.g., phlogiston and caloric fluid. One kind of
cognitive representation concept, the sententially-structured folk
psychological one, will be replaced by a different cognitive representation
concept emerging from developing neuroscience. This is exactly the result
that obtained in historical revisionary reductions. Relativity theory still posits
a length concept, a mass concept, and a velocity concept: just not the
specific ones from classical mechanics. If a revisionary intertheoretic
reduction obtains between folk psychology and some neuroscientific
successor, it will yield significant conceptual change that will rule out strict
cross-theoretic identities. But it will not yield wholesale elimination of the
caloric fluid/phlogiston variety.
An IR reformulation grounded on Hooker’s theory of reduction
suggests a promising approach for addressing the traditional mind-body
problem. Perhaps it afford resources that can break the impasse stressed
in section 1 above. But at least two big problems remain. First, we’ve seen
nothing in the IR reformulation presented so far that addresses the most
influential criticism in the philosophical (and cognitive-psychological)
literature against the possibility of psychophysical reduction: the "multiple
realizability" argument . Second, Hooker’s theory of reduction is subject to
serious criticism from within the philosophy of science. It is handwaving
about detailed applications to historical cases (and silent regarding detailed
applications to current psychophysical cases), leaving the key notion of an
analog structure IB without a clear illustration. And as Hooker (1981) himself
admits, his concept of the analog relation between IB and TR lacks precise
formulation. Without some answer to these shortcomings a Hooker-inspired
IR reformulation remains problematic. What can be said in its defense?
6. Handling Multiple Realizability
Just as intertheoretic reduction was being brought to bear on the
issue, Hilary Putnam and Jerry Fodor (among others) were emphasizing the
problem that multiple realizability raises for psychoneural reduction.
(Putnam published a number of papers throughout the 1960s that developed
this theme; key ones are reprinted in his 1975 collection. Fodor extended
these arguments in his 1974 essay and the first chapter in his 1975 book.
Bickle 1999 reviews key themes in the literature, but see Bickle 1998,
chapter 4, for a more detailed, technical discussion.) The contention is that
a given mental type (property, state, event) is realized by a variety of
distinct physical kinds sharing nothing of significance at that level of
description. Putnam’s now-familiar example was pain (see especially his
1967 essay): the same pain state seems ascribable to creatures with very
different nervous systems (humans, rats, octopi, and so on), and perhaps
even to beings lacking terrestrial nervous systems (silicon-based space
aliens, appropriately programmed digital computers). But then any
postulated type-identity or "reduction" of pain to any one of its multiple
physical realizers is false.
Not only was multiple realizability the central premise in influential
arguments against early mind-brain identity theories; it also served indirectly
in arguments for functionalist theories of mind. (Fodor 1981, "Introduction,"
describes this connection nicely.) And although functionalism has by now
been by and large replaced by nonreductive physicalism as the dominant
theory of mind in Anglo-American philosophy, proponents of the new
orthodoxy adopt uncritically the functionalist multiple realizability criticism of
psychophysical reductionism (see, e.g., Horgan 1993). So the question that
any proposed IR reformulation of the mind-body problem must answer is:
Do any recent accounts of intertheoretic reduction skirt the multiple
realizability challenge?
First, notice that if multiple realizability is a premise in a sound
argument for functionalism, the IR reformulation proposed above finds a
place for that theory of mind. Functionalism emerges as the prediction that
folk psychology will reduce rather smoothly to a functionally-specified
cognitive/computational psychology, with the latter remaining autonomous
from lower-level physical sciences (perhaps due to multiple realizability).
Fodor (1981) seems to have exactly this picture in mind when he lists some
"common sense psychological etiologies" and urges their lesson:
Seeing that a is F is a normal cause of believing that a is F; the
intention that it should be the case that so and so is a normal
cause of actions whose goal is to bring it about that so and so;
statements that P are normally caused by beliefs that P . . . The
point of such examples is not, of course, that any of them are likely
to figure in serious cognitive psychology. It is rather that our
attempts at a serious cognitive psychology are founded in the
hopes that this kind of generalization can be systematized and
made rigorous. (pp. 25-26)
A smooth intertheoretic reduction of folk psychology (qua collection of
"common sense psychological etiologies") to a "serious cognitive
psychology" would be one clear way to "systematize and make rigorous"
this kind of generalization. So even if multiple realizability establishes the
autonomy of psychology (folk or scientific) from physical sciences, this fact
alone would not nix an IR reformulation of the traditional mind-body
problem. Indeed, this fact can be accommodated within it.
Still, the IR reformulation has obvious roots in physicalist reduction
projects. We saw in sections 1 and 2 above that the approach is motivated
by the attempt to bring the mind within the scope of physical science. Can
psychophysicalism be salvaged from the multiple realizability challenge by
adopting some alternative approach to intertheoretic reduction?
Some early replies to Putnam and Fodor utilized resources from
theories of reduction. Robert Richardson (1979) pointed out that Nagel
(1961) himself countenanced conditional bridge principles in intertheoretic
reductions. Although Nagel’s examples employed biconditional bridge
principles, all the "connectability" that his condition of derivability required
was one-way conditionals: For all x, if Bx [predicate of reducing TB], then
Rx [predicate of reduced TR]. And conditional bridge principles are
consistent with the multiple realizability of TR types: as B’ in TB’, B’’ in
TB’’, and so on.
Another popular reductionist reply rested upon an insight first noted by
David Lewis (1969). Intertheoretic reductions are typically domain-specific.
Berent Enç (1983) and Patricia Churchland (1986), among others, have
pointed out that domain specificity obtains in the "textbook" reduction of
classical thermodynamics-to-statistical mechanics and microphysics.
Temperature in a gas is mean molecular kinetic energy. Temperature in a
solid is a different statistical mechanics/microphysical property, mean
maximal molecular kinetic energy, because the molecules in a solid are
bound up in lattice structures and are restricted to a variety of vibratory
motions. Temperature is multiple realized in distinct statistical
mechanical/microphysical states, and yet it is a central reduced kind in the
paradigm case from the history of science. Clearly, multiple realizability
alone is not enough to block an intertheoretic reduction. Jaegwon Kim
(1993) builds domain specificity directly into his very concept of reductive
bridge principles. In "local reductions" cross-theoretic bridge principles have
the form, "For all x, if Sx, then Bx if and only if Rx," where S is a predicate
denoting a type of structure in the appropriate branch of science. Different
Bs (typically) occur in the embedded biconditional for different structure
types, accommodating multiple realizability. According to Kim, local
reductions "are the rule rather than the exception in all of science, not just in
psychology" and are "reductions enough . . . by any reasonable scientific
standard and in their philosophical implications" (1993, p. 257).
However, this strategy does not handle all types of multiple realizability.
Since Fodor (1974), psychophysical anti-reductionists have emphasized a
more radical sense of the relation. Call the sense introduced by Putnam "
multiple realizability across physical structure types": distinct types of
physical structures realize a given mental kind differently. The domain
specificity reply undercuts an anti-reductionist argument built on this sense.
But now consider "multiple realizability within a token system across times":
a single instance of a cognitive system might realize a given mental type in
different types of physical states at different times. (The terms for these
two senses are from Bickle 1998, chapter 4.) The plasticity of mammalian
brains—in responding to trauma, changing task demands, developmental
processes, and the neural mechanisms of learning—suggests that this more
radical sense of multiple realizability is genuine. Ned Block (1978) once
suggested that narrowing the scope of psychological generalizations to
handle Putnam’s sense of multiple realizability (by way of the domain
specificity approach just discussed) would render legitimate comparative
psychology across species problematic (not to mention routine
methodologies in experimental psychology using animal models!). But a
psychology narrowed enough in domain specificity (scope of applicability) to
handle this more radical sense of multiple realizability—generalizations
applicable only to individuals at times—would surely render it insufficient to
accommodate even the most minimal assumed generality of science.
Appeals to scientific practice and history can give the physicalist some
ammunition against arguments built on this more radical sense of multiple
realizabiltiy. Pertaining specifically to psychoneural reduction, Kim (1993,
chapter 16) and Bickle (1998, chapter 4) point out that a guiding
methodology in contemporary neuroscience assumes continuity of
underlying physical mechanisms both within and across individuals and
species. This assumed continuity is more than a mere analogy, especially at
the level of cellular and molecular neuroscience, and informs most
experimental techniques, research paradigms, and theoretical conclusions.
(Special techniques also exist to control for idiosyncratic activity on
individual trials: e.g., subtraction techniques in PET (Positron Emission
Tomography) imaging. See Posner and Raichle 1994.) If the radical sense
of multiple realizability really obtained to the degree stressed by
anti-reductionists, the experimental techniques of contemporary
neuroscience would have borne little fruit. But clearly these techniques are
effective and not hopelessly naïve, and this is evidence that the kinds
postulated by psychological theories might not be as radically multiply
realized as anti-reductionists imagine. Why has a detailed study of the
macaque’s visual system been so instructive for learning about the
human’s? Why has PET and functional magnetic resonance imaging (fMRI)
revealed common areas of high metabolic activity across and within
individual humans, down to a resolution of less than 1 mm (and promising to
go lower as techniques and analytical tools improve)? (See Posner and
Raichles 1994.) Even neural plasticity is a systematic process. It follows a
regular progression both during development and following damage to a
principal structure. There are underlying neural mechanisms that subserve it
in all its forms, and the cellular and molecular mechanisms are shared
across a wide variety of creatures (Kandel and Squire 1999). In addition,
function is often compromised following serious neural damge. Persons can
still, e.g., talk, manipulate spatial representations, or move their limbs, but
their performance is typically degraded. This fact gives rise to tricky
questions about individuation of mental types. Do these distinct pre- and
post-plasticity neural events realize the same mental kind?
Appealing to science generally, Enç (1983) and Bickle (1998) suggest
that this radical sense of multiple realizability is also present in historical
cases of intertheoretic reduction, including the paradigm classical
thermodynamics-to-statistical mechanics and microphysics case. For any
token aggregate of gas molecules there is an indefinite number of
microphysical realizations of a given temperature: a given mean molecular
kinetic energy. So even this radical sense by itself appears not to block an
intertheoretic reduction. (Bickle 1998, chapter 4, also argues that exactly
this sense of multiple realizability is emerging between propositional attitude
and cognitive neuroscientific/"connectionist" theories of representational
content.)
So proponents of the IR reformulation can adopt the following attitude
toward the multiple realizability challenge, expressed eloquently by Hooker:
It is often argued that, e.g., cognitive psychology cannot be
reduced to neurophysiology because the former cross-classifies
the latter: any number of different systems (from brains to
machines to leprechauns passing notes) could realize the same
functional or computational theory. It helps to remove the
intellectual dazzle of this fact to realize that this is true of any
functionally characterized system. The same cross-classifications
turn up within such prosaic fields as electrical engineering (cf. "is
an amplifier of gain A" vis-à-vis particular circuit diagrams) and
physics (cf. "is a high energy electron source" vis-à-vis quantum
specification). (1981, p. 505)
(Notice that at least the latter case clearly admits of indefinite realizations in
the same token high energy electron source over time: the more radical
sense of multiple realizability). The key is a better understanding of
intertheoretic reduction across all of science. Hooker continues: "In these
cases, the issue is not whether reduction is possible, but how it goes. The
same applies, I hold, between theoretical domains as well" (1981, p. 505).
According to Hooker, any theory of reduction must handle multiple
realizability of reduced on reducing kinds. Any theory that does not is
insufficient for science generally, not just for the cognitive and brain
branches.
This section is not intended to be a comprehensive review of the
multiple realizability literature and its implications for philosophy of mind. All
that I have attempted to do here is to indicate ways that alternative
approaches to reduction in the philosophy of science and their application to
philosophy of mind can address some of the issues. Establishing that
multiple realizability does not spell immediate doom for IR- reformulated
psychophysical reductionism is enough for my present purposes. But this
brings us now to the crucial step: is there an account of intertheoretic
reduction that is sufficient for science generally and capable of handling the
special complexities raised by potential psychology-to-neuroscience
reductions? Or is the IR reformulation ultimately a hopeless approach for
addressing the traditional mind-body problem?
7. New Wave Reduction
Up to this point I’ve stressed the advantages of Clifford Hooker’s
account of intertheoretic reduction as the basis for an IR reformulation of
the traditional mind-body problem. Now it is time to address the
shortcomings. Although Hooker (1981) mentions numerous historical cases
of scientific reduction in presenting his theory, he never applies it to the
quantitative details of any particular example. Nor does he analyze the
concept of the "analog structure" IB much beyond the simple schema
presented in section 5 above. This lack leaves this central notion in his
account mysterious. Second, as he himself reluctantly admits, he is unable
to give a precise formulartion to his equally central concept of the "analog
relation" between IB and TR. This latter concept grounds Hooker’s idea
about the "amount of correction" implied to TR via its reduction, and in turn
the entire intertheoretic reduction spectrum between "smooth" and "bumpy"
cases. He writes: "Unhappily, I can think of no neat formal conditions which
would intuitively separate the two" (1981, p. 223). He hints that
"category-theoretic methods" might ultimately give some quantitative
account of "comparative preservation indices" for a theory’s "theoretically
relevant properties," and subsequently for its posited entities and events
(1981, p. 224). But he admits that "all of this is very programmatic and as
yet lacking in deep yet simple insight" (1981, p. 224). To date, Hooker has
not returned in print to this lacuna.
Bickle (1998, chapter 2) takes on this first shortcoming by
reformulating in Hooker-reduction terms the mathematical derivation of the
classical ideal gas law (pV = nrT) from Avogadro’s hypothesis, the
universal gas constant, kinetic-theoretic assumptions about the nature of
microparticles, and principles of Newtonian mechanics. A step of
mathematical rearranging to standard treatment of this derivation yields an
equation containing only quantitative expressions from statistical mechanics
and microphysics that mimics exactly the ideal gas law (Bickle 1998, pp.
34-39). Although the mathematical details are beyond the scope of this
essay, this result gives a clear example of the structure of an IB in an actual
scientific case. Happily, it also illustrates a case that lies midway between
the "smooth" and "bumpy" endpoints on the intertheoretic reduction
spectrum.
However, the second shortcoming is less tractable using the resources
Hooker himself develops. To address it, Bickle (1998, chapter 3) proposes
adopting a fundamentally different account of theory structure. He draws on
work from the "structuralist" program in philosophy of science, initiated by
Joseph Sneed (1971) and Wolfgang Stegmüller (1976) and developed most
completely and rigorously in Balzer et al. (1987). This program builds upon
earlier developments of the semantic view of theories (Suppes 1956, 1965),
which characterized theory structure not as a set of sentences or
propositions but rather as a set of models meeting specific set-theoretic
conditions. (See the brief discussion in section 4 above.) The structuralist
literature on intertheoretic reduction contains two principal accounts, one
constructed self-consciously to capture Nagelian intuitions (Balzer et al.
1987, chapter 5), the other constructed to capture Thomas Kuhn’s
alternative (Mayr 1976). Bickle’s goal was to build Hooker’s concept of
the analog structure IB, once illuminated by the detailed quantitative
application to the classical thermodynamics-to-statistical mechanics and
microphysics case mentioned in the previous paragraph, into the basic
structuralist account. His proposed result is a precise, semi-formal account
of "location on the intertheoretic reduction spectrum." The structuralist
concept of a "blur," extended by Bickle to apply to intertheoretic relations,
even provides a rough cardinal estimate of the "amount of correction"
implied to TR in specific cases. Application of another structuralist resource,
"ontological reduction links" (Moulines 1984), even provides the account with
an answer to an objection that Schaffner (1967) leveled against related
set-theoretic accounts of reduction. In a later chapter, Bickle seeks to
reconstruct semi-formally parts of the reduction of a schematic propositional
attitude psychological theory to a connectionist-inspired counterpart (1998,
chapter 5).
The technical (set-theoretical) details of Bickle’s account are complex
and beyond the scope of this essay, but the basic intuition behind the details
is straightforward. Instead of characterizing intertheoretic reduction in terms
of syntactic derivations, the "new wave" approach construes the relation as
the potential constructability of an image of (the set-theoretic structure of)
TR within TB. New wave psychoneural reductionism is the prediction that as
psychology and neuroscience develop matured theories, this "constructable
image" condition will obtain. Evidence for this prediction is the fact that this
relationship is obtaining already, in recent (and still sketchy) cognitive
psychological and neuroscientific theories. (Bickle 1998, chapter 5, cites
some details of the "learning-long-term potentiation" link as an actual case
in point. In Bickle forthcoming he extends this treatment to more recent
discoveries from cellular and molecular neuroscience.) The upshot is that
the challenge Hooker (1981) was unable to meet can be addressed when
his insights about reduction are reconstructed and extended within an
alternative model of scientific theory structure.
"New wave" reductionism and its IR reformulation of the traditional
mind-body problem is a viable approach—and at present, the most fully
developed one—for defending psychophysical reduction. It is the current heir
to the tradition running from U.T. Place and J.J.C. Smart through Ernest
Nagel and Paul Feyerabend to Kenneth Schaffner, Clifford Hooker, and Paul
and Patricia Churchland (to name just a few). In the best tradition of
scientifically-informed philosophy, it seeks to weave together both
philosophy of science and the best current science itself, and to apply the
resulting mosaic to more traditional questions of perennial philosophy:
specifically, the mind-body problem.
 Top of
page
Top of
page
|