The Effect of Mind upon Brain
Henry P. Stapp
Lawrence Berkeley National Laboratory
University of California
Berkeley, California 94720
Abstract
A physics-based understanding of how our conscious thoughts can affect our physically described brains is described. This understanding depends on the shift from the mechanical conception of nature that prevailed in science from the time of Isaac Newton until the dawn of the twentieth century to the psychophysical conception that emerged from the findings of Planck, Bohr, and Heisenberg.. This shift converted the role of our conscious thoughts from that of passive observers of a causally closed physically described universe to that of active participant in an essentially psychophysical understanding of nature.
1. The Basic Question and Why It Is Important.
Science’s conception of the physical world changed radically during the twentieth century. At the end of the nineteenth century most scientists still viewed the physical universe as essentially a giant machine. This mechanical view emerged from the seventeenth century work of Isaac Newton, who built his conception of nature on the ideas of René Descartes. According to Descartes, the universe is composed of two kinds of elements, the first consisting of elements each of which occupies at each instant of time a definite region in space, and the second consisting of elements that include our human thoughts. Descartes allowed these two parts of nature to interact causally within our brains, but Newton specified that the motions of the elements of the first kind are completely determined by laws of motion that refer exclusively to elements of this first kind. In Newtonian-type physics these elements are, moreover, essentially mechanical, in the sense that they have been stripped of the experiential qualities that characterize our thoughts, namely the conscious awareness of feelings, and the capacity to grasp meanings. Consequently there is in Newtonian-type physics no possibility for any causally effective role for any aspects of our being that are essentially different in kind from the mechanical elements that occur in that type of physics. Descartes’ views accommodated our intuitive feeling that our conscious thoughts can influence our bodily movements---my conscious intent to raise my arm seems to cause my arm to rise---whereas Newton’s physics leads to the contrary conclusion that, in spite of what may seem to be the case, the notion that human thoughts, per se, can affect human actions is a deeply misleading illusion.Newton’s ideas led eventually to the classical physics of the late nineteenth century. Its main premises are these:
-
There exists a material universe that develops over the course of time by means of interactions of its tiny mechanical parts with neighboring tiny mechanical parts.
-
These interactions are governed by mathematical laws.
-
These laws entail that the mechanically described future is completely determined by the mechanically described past, with no reference to human thoughts, choices, or efforts.
This conclusion is called: The principle of the causal closure of the physical.
This “Principle” seemed at one time so secure, and so central to the scientific enterprise, that some scientists came to view science as not essentially an open-minded empirically based inquiry into the structure of nature, but as also an ideology: i.e., as the idea that scientists must be tenacious defenders of the dogma that we human beings are essentially material/mechanical systems governed exclusively by matter-based laws, and hence that our conscious thoughts and intentions can have no actual effects upon our physical actions: that the universe is, with respect to its basic causal structure, completely mindless.
This dogma blocks rational action: One cannot rationally choose to act to achieve a physical effect if one truly believes that one’s conscious choices can have absolutely no physical effects: One cannot act completely rationally while truly believing the materialist dogma!
Within that earlier pre-twentieth-century science-based conception of nature the existence of our streams of conscious thoughts constituted a major embarrassment. The occurrence of things having the defining characteristics of our conscious thoughts was in no way entailed by the properties of the physical world that the physicists had postulated. Our thoughts, ideas, and feelings could be imagined to be produced – in some unexplained way – by the complex activities of our brains. But there was no logical basis in the classical physicists’ conception of nature for understanding or explaining the emergence of human experience. Although philosophers wove endless tapestries of words in an effort to relate the physically described aspects of the world to the experientially felt aspects of our lives, the efforts of those thinkers were invariably judged inadequate by their critically minded colleagues. Insofar as our brains were understood exclusively in terms of the concepts of classical physics a causal gap persisted: a conceptual chasm remained between, for example, a painful feeling and the associated activities – no matter how complex and novel – of the associated physically described body and brain.
During the twentieth century this classical-physics-based conception of the world was found to be logically incompatible with a growing accumulation of empirical data. Eventually, the classical mechanistic description of the physical aspects of nature was replaced by the profoundly different quantum mechanical description.
The orthodox formulation of quantum mechanics, which is the form used in all practical applications, was created by Heisenberg, Bohr, Pauli, and Born during the 1920’s. Shortly thereafter it was cast into a more rigorous logical and mathematical form by the logician and mathematician John von Neumann.
Quantum mechanics differs from classical mechanics in deep mathematical ways. In order to tie the new mathematical structure to empirical data in a practically useful way the founders of quantum mechanics instituted a profound break with one of the basic principles of classical physics: they inserted the conscious experiences of human beings into the dynamical workings of the theory. Human beings were allowed, and indeed required, to act both as causally efficacious agents, and also as causally efficacious observers. In particular, orthodox quantum mechanics requires every conscious observation to be preceded, logically, by an action that specifies a ‘Yes-or No’ question, which a feedback “observation” will then answer either by a ‘Yes’ or by a ‘No’. Both of the two actions, the query and the feedback, are causally efficacious: they alter in different non trivial ways the physically described state of the universe.
Each of these two actions is described in two different ways. Each action is described first in the psychological language that we use to communicate to each other, and to ourselves, the structure of our experiences. And it is described also in the mathematical language of quantum physics. Each psychologically described event becomes thereby linked, within the theory, to the quantum mathematical description of the physical world. This dualistic---psychophysical---description was needed to link the quantum theoretical description of the mathematically controlled evolution of the physically described world to the structure of the communicable human experiences that constitute the empirical basis of science.
In this quantum mechanical description the unfolding of the universe is no longer governed by the physically described aspects of nature alone. Neither of the two actions, neither the query nor the feedback, is determined within the orthodox theory by prior physically described sufficient conditions. Within orthodox quantum mechanics, our causally efficacious conscious intentional efforts remain “free” of any specified physical coercion. Yet these conscious efforts do have, according to quantum mechanics, important physically describable effects. Quantum mechanics thereby rescinds the materialist dogma: it fails to validate/vindicate/support “the principle of the causal closure of the physical”! But in spite of this loss of its scientific support, the classical materialist ideology, including the precept of causal closure of the physical, continues to infect the thinking of many scientists and philosophers: the materialist ideology has survived the death of its body of scientific support
But why are these seemingly arcane matters important? Why, in the context of the pressing contemporary concerns of the human race, is attention to these scientific issues worthwhile? It is profoundly worthwhile because science’s pronouncements on the nature of our own human beingness, and on the character of the connection of our conscious intentional efforts to the unfolding physical reality, underlie much of the rational discourse on urgent societal issues.
The classical-physics-based conception of human beings has had a tremendously pernicious impact on our cultural heritage, because it paints us, on the one hand, as mechanical automata, whose consciousness intentional efforts can have no causal effects whatever on the physically described aspects of nature, and, on the other hand, as mechanical consequences of a dog-eat-dog competition for survival. The consequence of the first effect is to discourage conscious effort improve the human condition as pointless and irrational; and the consequence of the second effect is to justify unrestrained self-aggrandizement at the expense of the essential well-being of others. The materialist dogma undermines the foundations of moral and ethical philosophy.
Our beliefs about our relationship to the world around us underlie our values. And our values determine the sort of world we strive to create. The main social problems we face today stem primarily from the fact that different approaches to this basic question of our place in nature lead to different conclusions, and hence to conflicting values, and thence to conflicting actions. Because of the stature of science in contemporary culture it is vital to answer as accurately as possible the question: What does contemporary basic physics say about the nature of the connection of our conscious thoughts to the physically described aspects of nature?
2. From the Classical to the Quantum Mechanical Conception of the Role of Human Beings in the Unfolding of Reality.
Quantum mechanics rests upon a mathematical foundation provided by classical mechanics. The latter rests upon the idea of ‘particles’ and ‘fields’. A particle is supposed to have, at each instant of time, a definite position and a definite velocity in three-dimensional space. A field is supposed to have, at each instant of time, and at each location in three-dimensional space, a definite ‘value’, specified by a real number. The field variables are connected to the particle variables in way that determines the forces upon – and hence acceleration of – each particle, due to the presence and the motions of the other particles. These positions and numbers, together with few constants that determine such things as the masses of the particles and the strengths of various forces, constitute the physical aspects of nature.
Newton conjectured the existence of repulsive forces that prevent particles from coming too close to each other. This condition combined with his other laws appears to entail ‘the causal closure of the physical’: the description of the physical aspects of nature over some short interval of time, combined with the physical laws, completely determines all physical aspects of nature for all times.
This closure feature allows the evolving state of the universe to be pictured as block physical universe; namely by a collection of particle trajectories---conceived as infinitely thin ‘wires’---running through the space-time, in the direction of increasing time, and in a way that is uniquely determined for all times by the form of this physical structure over any short interval of time. (The ‘fields’ should also be represented, but their pictorial image is slightly more complicated.) In Newtonian-type mechanics no representation of experience or knowledge need be considered. That is why this feature of Newtonian-type physics is called ‘the causal closure of the physical.’
The transition from classical---Newtonian-type---mechanics to quantum mechanics brings human knowledge and experience importantly into the theoretical framework. The reason, basically, is this: the way the mathematical/physical description enters into practical applications is closely analogous to the way that the mathematical/physical description enters into classical statistical mechanics. But classical statistical mechanics is, in its practical applications, closely tied to human knowledge: A sudden change in “our knowledge” causes a sudden change in the mathematical/physical representation of our knowledge, which produces in turn a sudden change in the knowledge-based predictions of the theory.
Classical statistical mechanics accommodates in a completely understandable way our uncertainties about the actual positions and velocities of the physical particles. An analogous feature of quantum mechanics is the ‘Heisenberg Uncertainty Principle’. The effect of this principle is, essentially, to convert each ‘wire’ of the block universe picture into a smear of weighted possibilities. More precisely, for a many-particle universe, the effect of the Heisenberg uncertainty principle is to replace the one single actual many-particle universe of classical Newtonian-type physics by the collection of all such (weighted) possibilities compatible with the present state of ‘our knowledge’. This smearing out of the set of possibilities can be large at the level of the atomic particles. Then, because of the sensitive dependence of macroscopic degrees of freedom upon microscopic initial conditions, the so-called butterfly effect, the smearing out at the macroscopic level tends to increase with the passage of time. Yet at certain moments we gain, via our (sense) experiences, new knowledge. Just as in classical statistical mechanics, this new knowledge will usually exclude some of the possibilities that were mathematically generated from an earlier state by the mechanical equations of motion This sudden gain in knowledge will be represented by a sudden ‘collapse’ of the mathematical representation of the state of our knowledge to a ‘reduced’ form: to a ‘reduction’ of the size of the ‘wave packet’.
This reduction of the size of the physically described wave packet is tied, just as it is in classical statistical mechanics, to the increase in our knowledge. For example, if we originally know only that a particle is in a certain box, and then learn, from some observation that we make, that the particle is definitely not in the right-hand half of this box, then the region over which the weighting factor is non-zero is ‘reduced’ to the left-hand half of the box. This reduction, combined with our knowledge of how the physical state evolves during the intervals between our observations, will alter our expectations about our future experiences.
There is nothing at all mysterious about such sudden ‘collapses’ in classical statistical mechanics. The ‘collapses’ that occurs in quantum mechanics are, at the level of actual scientific practice, quite analogous to it: in both cases the mathematical representation of ‘our knowledge’ changes abruptly when ‘our knowledge’ changes abruptly. It is this close correspondence---at the level of actual scientific practice---of quantum mechanics to classical statistical mechanics that allows scientists to use quantum mechanics in a rationally coherent that they can understand intuitively.
But there is a conceptual problem: in quantum mechanics the different ‘classically conceived possibilities’ can interfere with each other in ways that they cannot do in classical statistical mechanics. According to the precepts of classical statistical mechanics, all but one of the various weighted possibilities exist only as figments of our imagination, and the one real situation cannot be affected by possibilities that exist merely as imagined possibilities---which we have found useful to contemplate because of our lack of knowledge about which of the possibilities allowed by the physical theory is the unique one that really exists. Classical statistical mechanics demands, accordingly, that the various possibilities evolve independently of each other, in the way physically specified by the underlying classical mechanics. This postulated causal structure effectively blocks any causal effects of our human thoughts per se---which are characterized by conscious awareness, feelings, and understandings of meanings---upon the dynamical machinations of the physical aspects of nature. According to classical mechanics, these physical aspects are completely controlled exclusively by these physical aspects themselves, which have been completely stripped by the precepts of classical mechanics of those features that characterize our thoughts. From the standpoint of classical physics, our strong intuitive feeling that our thoughts themselves can affect the physically described world must be deemed a misleading illusion.
The claim of classical physics that there is this causal disconnect between the mental and physical aspects of nature is so peculiar and unnatural as to render nearly irresistible the idea that this physical theory must be an approximation eventually to be superseded. Although some thinkers continue to cling steadfastly to the precepts of nineteenth century classical physics, which automatically enforce the very approximation that needs to be undone, those precepts were shown already during the first part twentieth century to be incompatible with empirical findings, and to be, moreover, indeed an approximation to a more adequate physics---quantum physics---that does in fact feature essential dynamical links between these two aspects of nature.
The resolution of the conceptual problem mentioned above is to interpret the quantum mechanically described state of the universe as a representation not of imagined physical possibilities, but rather of ‘potentialities for future psychophysical events’: i.e., as a representation of objective tendencies, created by past psychophysical events, for the occurrence of future psychophysical events. This interpretation is essentially implicit in orthodox quantum mechanics, and was nicely described by Heisenberg (1958a,b). It transforms ‘our knowledge’ from a realm of realities deemed unable to causally affect the unfolding of material/physical/mechanical aspects of reality to an essential causal input into the unfolding of an integrated psychophysical reality.
Of course, science has always been about ‘our knowledge’ in a certain ultimate way. It is about what we can know, and how we can use what we know to affect what we will probably experience under the various alternative possible courses of action between which we are seemingly free to choose. However, the effect of Newton’s monumental work was effectively to banish the psyche of man from any causal role in the future of man. Consequently, quantum physics is, perhaps more importantly than anything else, a liberator of the human mind from the 200 years of bondage imposed, within science-based philosophy, by the huge achievements of Isaac Newton.
The main interpretive idea of orthodox quantum mechanics is that each acquisition of knowledge occurs discretely in conjunction with ‘a collapse of the quantum state’ to a new form that incorporates the effect of adding the conditions logically imposed by the increase in knowledge. This change forges a tight logical link between ‘an experientially recognized change in a state of knowledge’ and a corresponding ‘mathematically represented change in the physical state of the universe’. The new psychophysical state represents both a new state of knowledge and also a related new set of statistically weighted potentialities for future psychophysical events.
2.1.Von Neumann’s Shift of the Heisenberg Cut.
The original “Copenhagen” interpretation of quantum mechanics separated the physically described world into two parts: (1), the system being probed, which is considered to consist of atomic constituents described in the mathematical language of quantum mechanics; and (2), the rest of universe, which is treated as the ‘observer’, whose experiences pertaining to the observed macroscopic components of the world are described in the language of classical physics. This observing portion is supposed to include both the human observers and their macroscopic measuring devices, conceived and treated in the way that classical physics conceives and treats macroscopic objects. However, the macroscopic devices and the human observers are themselves composed of atomic constituents. Hence it is not clear where one should place the boundary between the part of the world that is described in terms of the quantum theoretical mathematics and the part that is described in terms of human experiences that can be expressed in terms of the language of classical (Newtonian-type) physics. There is no basic principle beyond practical utility that precisely specifies the placement of this “Heisenberg cut”.This question was studied by non Neumann (1932/1955), who showed, at least within the framework of suitably idealized cases, that the predictions of quantum theory are invariant under a shift of a macroscopic device from the classically described side ‘above’ of the cut to the atomistically described side ‘below’ the cut. By a series of shifts von Neumann includes more and more of the world in the part ‘below’ the cut, until at last the entire world that can be conceived to be built of atomic particles, including the entire brains of all the observers, are described in terms of the quantum mathematics. Thus Von Neumann examined the problem of where to place the cut by considering an idealized situation in which there is a sequence of measuring devices, each probing the output of the device that precedes it in the sequence, and by then following the causal chain first into the retina of the observer, and then into the optic nerves, and then ever deeper into the brain until at last the entire brain of the observer is treated quantum mechanically, along with the rest of the physical universe.
Yet quantum mechanics was formulated from the outset in terms of the relationship between the two different descriptions, the physical and the psychological. This dualistic structure continues to be maintained at each shift of the boundary, even when the entire physically described world is treated quantum mechanically. Indeed, what needs to be preserved at each step is essentially the predicted relationships between human experiences, which are described in psychological terms. The final part of the brain that remains just above the cut before the final shift is described in psychological and classical terms just before the final shift, but in atomic quantum-mechanical terms after that final shift. Von Neumann gives the name “abstract ego” to the carrier of the logically needed psychologically described aspects that must still remain even after all the brains of all the agents are described purely in physical terms. The theory at that stage describes the entire physical world quantum mechanically, with each psycho-physical event now specifying a particular action, associated with a definite spatial region and a certain definite time, that connects the mind and the brain of a conscious agent.
The nature of this psychophysical connection will be described presently. But the upshot is that this connection allows, and indeed seems to require, the psychological events that populate our streams of conscious experiences to play a dynamically active role in the determination of the temporal development of the physically described properties of our brains. This psychophysical connection, which is the focal point of this article, will now be discussed in more detail.
2.2. The Basic Conflict Between Classical and Quantum Physics.
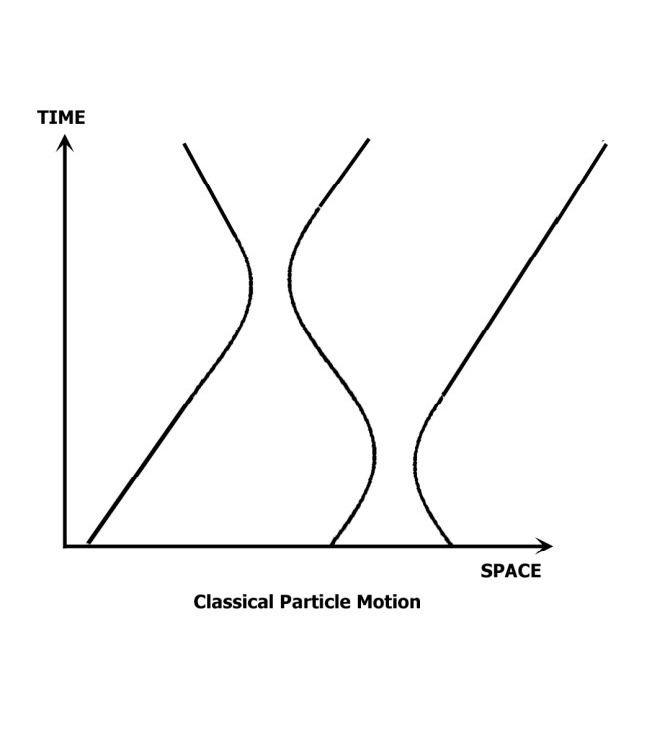
Classical mechanics assumed that the ideas that work well for large objects, such as planets, moons, and falling apples, will continue to work all the way down to the level of the atoms and molecules. According to this classical notion, each particle, such as an electron, has a well defined trajectory in space-time. This idea is illustrated in figure 1.
Figure 1. Classical Physics. This diagram shows a possible evolution in time of a system consisting of three classically conceived electrons. Each particle has a well defined trajectory in space-time, and each particle repels the others increasingly as their trajectories come closer together.
The laws of motion of classical physics ensure that the trajectories of all the particle (and fields) in the universe at times earlier than some fixed time t fix the trajectories of all particles for all future times.
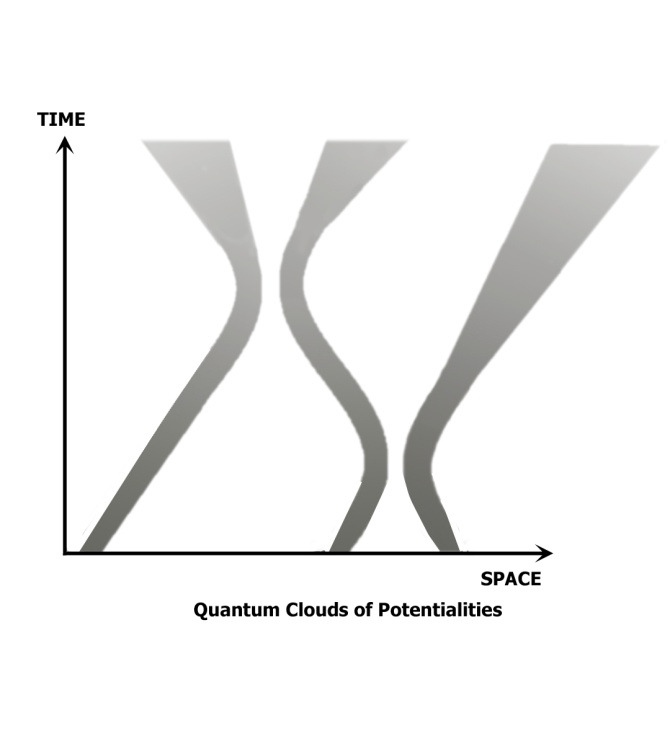
A principal change introduced by quantum theory is the “quantum uncertainty principle”. This principle asserts that each particle must be represented, NOT by one single well defined trajectory, but by a cloud of possible trajectories, as is shown in figure 2.
Figure 2. The quantum cloud. This diagram illustrates the usual effect of ‘quantizing’ the classical system shown in Figure 1. Each trajectory line of the classical theory is broadened out into a cloud of alternative possible trajectories, as a consequence of the uncertainty principle.
The effect of these uncertainties, if left unchecked, would be disastrous. The uncertainties at the atomic level tend to bubble up, irrepressibly, to macroscopic levels. If the uncertainties originating at the micro-level were left unchecked from the time of the “big bang”, the macroscopic world would be by now a giant cloud encompassing all possible worlds, in stark contrast to the essentially single macroscopic world that we actually observe. For example, if the uncertainties were left unchecked then the moon would be spread out over much of the night sky; And each person’s brain would correspond to a mixture of all of the many alternative possible streams of consciousness that the person could in principle be having, instead of corresponding to the essentially single stream of consciousness that each of us actually experiences.
To deal with this difficulty the founders of quantum theory were forced to draw a clean conceptual distinction between the two aspects of scientific practice, the empirical and the theoretical, and to introduce a special process to account for their connection. The empirical component describes our experiences pertaining to what we human beings do, and to the experiential feedbacks that we then receive. The theoretical component describes the “particles and fields”. The process that connects these two aspects of the scientific description of the world is called the process of measurement or observation.
This measurement/observation part of the quantum mechanical approach erects a firewall that protects the empirical/experiential realm from an unfettered intrusion of quantum uncertainties from the theoretical realm.
2.3. The Firewall that Protects the Empirical Realm from the Quantum Uncertainties that pervade the Physical Realm.
But how are the quantum uncertainties held in check? The theory of the process of measurement was put into rigorous form by John von Neumann, building on ideas of Werner Heisenberg.
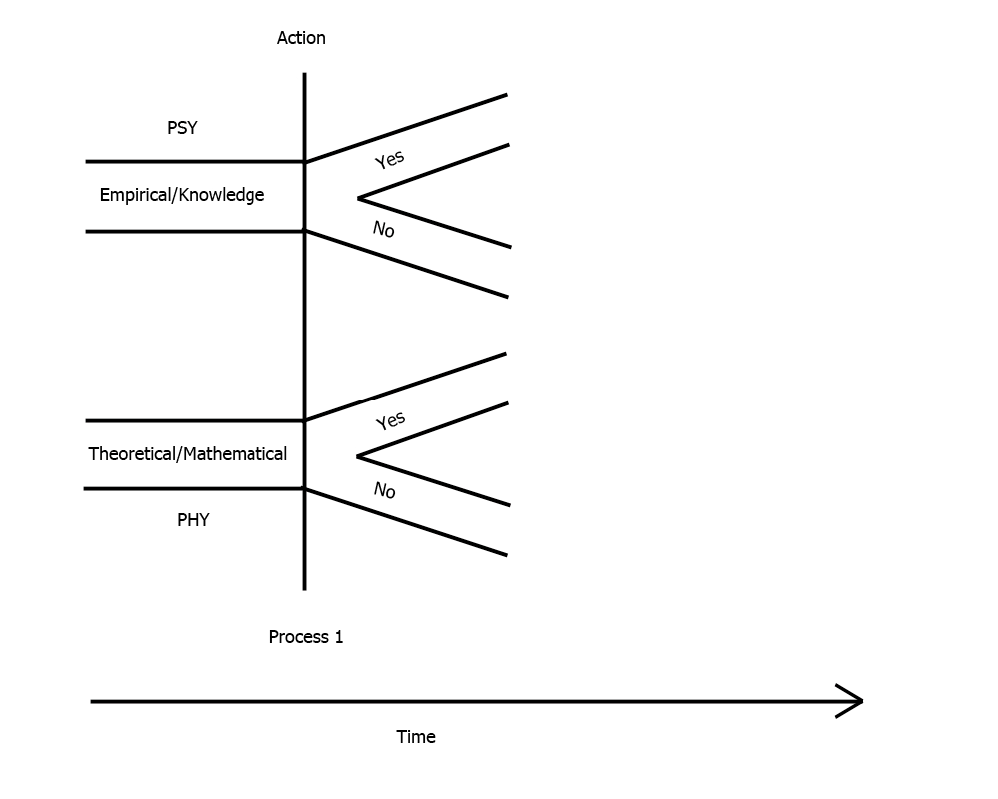
The theory demands that each experience occur in conjunction with an associated intervention into Schroedinger-equation-controlled evolution of the physical state. This intervention is called “process1” by von Neumann. This physical action is associated with a psychological element, which is a specification of a particular question that can be answered empirically by either a ‘Yes’ or by a ‘No’. (Multiple choice questions can be reduced to sequences of Yes-or-No questions).
The temporal evolution of the full reality is punctuated with these process-1related events. Each such event has two related aspects, one in the empirical domain of ‘our knowledge’, and the other in the domain of the mathematical description. On the empirical side the action specifies a certain possible “increment in knowledge”: an experientially recognizable ‘Yes’ response to the question. This ‘Yes’ answer is linked on the mathematical side, to a reduction of the prior quantum mechanical state to that part of itself that is consistent with the increase in knowledge corresponding to the answer ‘Yes’. This reduction is analogous to the similar reduction that occurs in classical statistical mechanics, as has already been explained.
If nature fails to deliver the answer ‘Yes’, then the prior physical state becomes reduced to the part of itself that is unambiguously associated with the answer ‘No’.
This action process is represented in figure 3.
Figure 3. The action associated with Process 1. Each empirical finding is associated with a process 1 quantum reduction event that has both an experiential part that represents a separation of the agent’s stream of consciousness into two particular alternative possible paths, labeled ‘Yes’ and ‘No’, The ‘Yes’ answer identifies an experimentally/empirically defined ‘Yes’ feedback to an agent-posed query There is a corresponding separation of the physical state into a ‘Yes” part and a ‘No’ part, with the ‘Yes’ part specifying the part of the prior physical state that is compatible with the agents having a ‘Yes’ experience.
Von Neumann calls the physical part of this action by the name “process 1”. Two important facts about process 1 are:
-
The process 1 actions enter importantly into the dynamics.
-
Quantum mechanics does not identify any logically sufficient physically described cause for this action!
Consequently, the “principle of the causal closure of the physical” is not entailed by the rules and content of orthodox quantum mechanics!
Von Neumann gives the name “Process 2“’ to the process that causes the quantum state to evolve according to the Schroedinger equation, which is the quantum analog to the classical deterministic equations of motion.
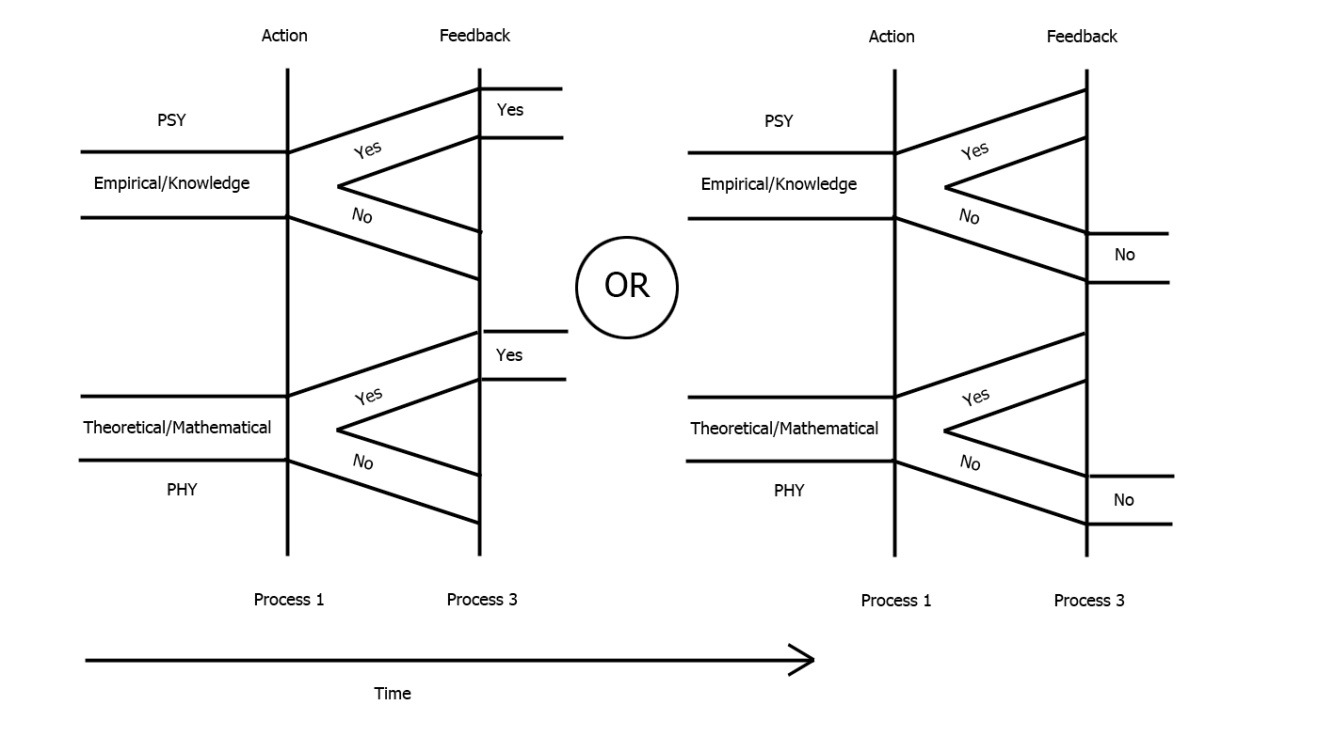
The measurement process has a second part: the Yes-or-No feedback from the associated action. This second stage is called ‘Process 3’, and is pictured in figure 4.
Figure 4. Process 3. Nature delivers a feedback ‘Yes’ or ‘No’ to the agent’s query.
According to quantum mechanics, the feedbacks conform to statistical conditions that are specified by the theory. The choice of the feedback (or outcome) is what Dirac called: “a choice on the part of nature”. According to quantum mechanics, this choice of outcome is statistical, and, unlike process 1, it lies outside the hands of human beings.
The choice of the process 1 probing action is what Heisenberg called “a choice on the part of the ‘observer’ constructing the measuring instruments and reading their recording.” (cf. Bohr, 1958. p. 51) As regards this choice Bohr says:
“The freedom of experimentation…corresponds to the free choice of experimental arrangement for which the quantum mathematical formalism offers the appropriate latitude.” (Bohr, 1958, p.73)
These remarks by the founders of quantum mechanics emphasize that the physically described aspects are, within contemporary physics, no longer dynamically complete, but have, in particular, a process-1-related dynamical gap that, at least in practical applications, is considered to be influenced by our consciously experienced intentions.
The process of measurement creates a firewall that blocks the unfettered diffusion of the quantum uncertainties into the empirical (or experiential) realm.
It is the choice of a process 1 action, which is not controlled by any known process, statistical or otherwise, but which appears to be influenced by understandings and conscious intentions, that, in conjunction with a stochastic process 3 choice of feedback on the part of nature, controls which potentialities pass through the firewall, and into the realm of our actual experiences!
I call the process, whatever it is, that chooses the form of process 1, and the time t at which the process 1 action occurs, by the name “Process Zero”. The fact that process zero is not determined by the physical laws of contemporary quantum theory constitutes a “causal gap” in that theory: it entails an apparent breakdown of the “principle of the causal closure of the physical”. The orthodox interpretation of the theory is designed for practical application, and it fills this causal gap at the physical level by allowing an intervention from the mental realm to create a filter/firewall that permits only certain definite thoughts to emerge from the uncertain indefinite prior physically described universe.
3. Template for Action.
Any intentional physical action, such as raising one’s arm, requires sending a temporally correlated sequence of neural signals to the muscles. So it is plausible that there is, in association with each intentional action, a corresponding spatio-temporal pattern of neural or brain activity that if sustained for a sufficient period of time will tend to cause that action to occur. I call this spatio-temporal pattern of brain activity a template for action. The action of the process 1 associated with this intentional action should preserve this template for action, and eradicate the possible patterns of brain activity that are incompatible with it.3.1. Process 1 and the Conversion of an Intentional Thought to a Bodily Action.
An experimenter’s action of setting up a particular experiment is an action directed at the goal of receiving an intended feedback. It is represented in quantum theory by a psycho-physical event. The psychological aspect is the felt intention to receive the intended feedback. The ‘Yes’ part of the physical aspect of the associated process 1 action reduces the state of the brain to the part compatible with the template for the intended action.
3.2. The Quantum Zeno Effect.
It is a consequence of quantum dynamics that sufficiently rapid repetitions of the same process 1 action can, by virtue of the so-called quantum Zeno effect, cause the template for an intended action to be held in place, in the face of strong disrupting physical forces, for much longer than would otherwise be the case. Such an extended holding-in-place of this template for action will tend to make the intended action occur. Thus influencing the repetition rate of a sequence of process 1 actions can influence the bodily actions of the agent.The repetition rate of a sequence of process 1 actions in a human brain is not controlled by the known quantum physical laws. Thus we are invited to consider the possibility that these repetition rates can be influenced by mental realities, and in particular by the psychological intensity of the conscious intention to perform the physical action associated with a template for action. Postulating such an influence creates the possibility of accounting causally, within contemporary physics, for the apparent connection of conscious intention to bodily action; a perceived connection upon which we base our entire lives. Classical physics, by restricting causal connections to a causally closed physical domain, with no conceptual foothold for any logical link to consciousness, provides no analogous possibility for rationally understanding a real effect of our conscious intentions themselves upon our physical actions..
The process zero, whatever it is, that determines the form and the timings of the process 1 actions is not the quantum mechanical process, process 2 (the Schroedinger equation controlled process) that governs the time evolution of the quantum state of the system. That quantum state, according to orthodox ideas – particularly those of Heisenberg – specifies only the potentialities/probabilities for the actual events, but neither the form nor the timing of the actual events themselves. The Schroedinger equation, which is a quantum mechanical analog of the equations of motion of classical mechanics, makes no reference at all to idea-like realities such as intentions or mental concepts. But this same limitation does not apply to process zero. Insofar as process zero allows the repetition rate for a sequence of similar process 1 actions to be influenced by conscious intentions, quantum mechanics provides a fundamental-physics-based way for our conscious intentions to bring the physical correlates of our conscious intentions into the physically described universe.
Quantum mechanics leads, therefore, to a radical revision of our conception of ourselves. Whereas classical physics reduced man to an essentially mindless machine, quantum mechanics allows a person’s conscious intentions to influence his physical actions.
Once this power of our consciously felt intents to causally influence the experienced feedbacks is introduced into the dynamics, the agents become enabled by trial and error learning to ingrain meaningful habits into their physical structures. But the physical effects of conscious feelings can be learned by trial and error only if conscious feelings have felt effects. This point is discussed in more detail in Stapp (2007).
3.3. Space-Time Structure.
We now look in more detail at questions that orthodox quantum mechanics does not answer: What determines when a process 1 action will occur, and what the form of the associated physical action will be? That is, we turn to the problem of understanding the possible workings of process zero. These questions pertain to the representation of process 1 in space and time.
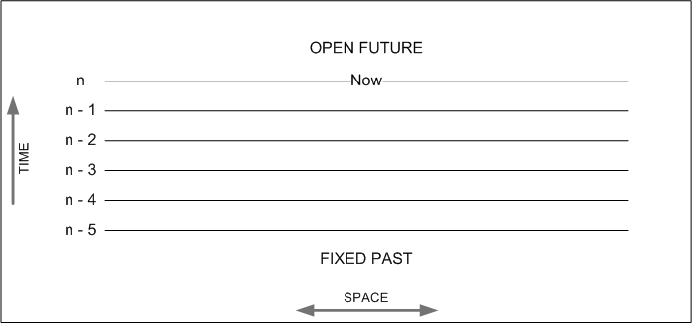
Von Neumann’s analysis was based on non-relativistic quantum mechanics. According to orthodox non-relativistic quantum mechanics, each collapse event occurs at an instant of time, and it changes the state of the extended-over-allspace system just before time t to the state of the system at the instant of time t. The horizontal lines in the figure shown below represent the instants at which the state of the extended-in-space systems suddenly changes.
Figure 5. A space-time diagram showing as horizontal lines the instants at which the evolving quantum state suddenly changes to a new (reduced) form. During the intervals between these times the state of the system evolves according to von Neumann’s process 2, the Schroedinger equation.
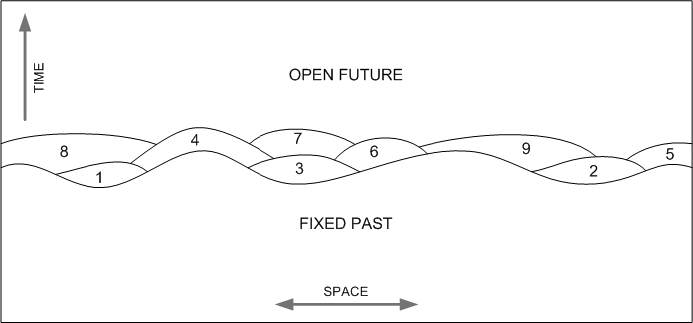
Von Neumann’s 1932 non-relativistic formulation was converted to a relativistic form during the middle of the century independently by S. Tomonaga (1946) and by J. Schwinger (1951). In this relativistic formulation the state of the system was associated not with an instant of time t, but rather with a space-like surface σ. A space-like surface σ is a continuous three-dimensional surface in space-time such that every point on the surface is space-like separated from every other point on the surface. A succession of collapse events can be assumed to occur on a succession of space-like surfaces σ such that each coincides with its predecessor except on a small patch, over which a surface σ is displace slightly into the future relative to its predecessor, as indicated in Figure 6.
Figure 6. The collapse events occur over a sequence of space-like surfaces σ each of which is locally shifted slightly forward in time relative to its predecessor. In the intervals between these surfaces the state ρ evolves in accordance with the relativistic quantum field theory (RQFT) generalization of the Schroedinger equation.
The conceptual structure of the theory remains unchanged: the physically defined quantum state represents not “actuality” itself, but rather a set of objective tendencies pertaining to the occurrence of the next psycho-physical event. It is these events, which are psychophysical entities, that are regarded as the objectively existing actualities.
3.4. Process Time.
The time represented by the vertical axis in figures 5 and 6 can be called “physical time”: it is the time that appears in our presently existing physical theories. But we can consider also another concept of time that marks, first, the stages of development associated with the region 1 of figure 6 and, next, the stages of development associated with region 2, etc.. I call this time by the name “process time”. [Stapp, 1985] This time is naturally accommodated by relativistic quantum field theory, which permits the space-like surface σ upon which the present state is defined to advance locally, rather than globally According to RQFT, the quantum (physical) state evolves via process 2 from the backside to the front side of each of the regions indicated in diagram 6. But we can allow the psychophysical process that determines what the process 1 reduction will be on the forward side of the region to develop in process time. In particular, RQFT allows the psychophysical processes associated with the various spacelike separated regions to occur in a definite sequence, as indicated in figure 6, and as marked by process time. RQFT then ensures that all predictions of the theory will be independent of the order in which space-like separated events occur in process time. For the discussion of such logical issues it seems helpful to introduce this concept of a well defined order of coming into being in process time that is logically prior to the less incisive partial orderings that occur in the theory of relativity, in which the order in which spacelike separated events occur is considered to be not only empirically undecidable, but--in keeping with certain positivistic precepts---also fundamentally undefined.4. Connection to Whitehead.
According to quantum mechanics, brain dynamics at the microscopic scale is subject to the uncertainty principle. This indefiniteness at the microscopic level tends to be magnified by the energy-releasing neuro-dynamics of the brain as one moves up to the macroscopic scale. Yet any gross indeterminacy at the macroscopic level conflicts with the empirical definiteness of our perceptions. A remedy is needed that will bring theory into alignment with experience.
The orthodox (Heisenberg/Bohr/von Neumann) remedy is a theory built on the idea that actuality is built of psycho-physical events, with the evolving quantum physical state interpreted as both a repository of information and as a ‘potentia’ for the occurrence of the next actual event. Each process-1 psychophysical event imbeds a correlate of a feature occurring in a stream of consciousness into the structure of the quantum mechanically described world, whereas each process-3 psychophysical event implants a correlate of a new piece of physical information into a stream of consciousness.
The idea of a reality built around localized psycho-physical actual events, and of ‘potentialities’ for them to occur, is the core of a conception of reality advanced also by Alfred North Whitehead. He was stimulated by quantum mechanics, but constructed his theory of a psychophysical-event-based reality within the framework of the ideas of the major figures of western philosophy. The central focus of Whitehead’s work is precisely on the processes that I am calling “process zero”, namely the process that formulates queries, and on the process that then chooses the answers to these queries, whose formulations and answers control the “creative advance into novelty”.
The conception of the process of the unfolding of reality provided by RQFT meshes neatly with Whitehead’s conception of the creative advance into novelty. One identifies each process 1 psycho-physical event and each follow-up process 3 psychophysical event with a Whiteheadian actual occasion. This identification ties Whitehead’s speculative philosophy into contemporary physics: it injects a science-based mathematical structure to the speculative philosophizing of Whitehead. On the other hand, orthodox quantum theory was specifically designed to be useful to human beings, and to be testable by them. Hence at that level it is manifestly anthropocentric. But within the Whiteheadian conception of process the human psychophysical events are considered to be mere special examples of the actual occasions that constitute the basic realities of the Whiteheadian creative advance into novelty. Whitehead’s ideas provide therefore a philosophically grounded framework for enlarging the anthropocentric focus of orthodox quantum mechanics.
Although the quantum psychophysical reality is dualistic, in the sense that it includes mental and physical properties within an integrated causal structure, it is not Cartesian dualistic because every occurrence of any thought-like property is tied to a space-time region, and in specified causal ways to the physical properties located in that region. There is therefore a blurring of the Cartesian categories, with every individually existing property, both physical and mental, localized in a particular space-time region. Properties expressed in terms of mathematically described understandings become, then, not so radically different from properties expressed in terms of psychologically described understandings. This blurring of the mind-matter distinction constitutes a drift away from a completely sharp dualism, toward the ‘radical empiricism’ of William James, or perhaps toward the ‘neutral monism’ of Bertrand Russell. (Russell, p.811, 1945)
Quantum mechanics was designed to account for the empirical regularities of our human streams of consciousness. Yet something was presumably going on before human beings arrived on the scene. So we are led to inquire about the nature of the quantum events that appear to lack the conscious dimension of the sort that we experience, but that appear to arise in purely mechanical ways. Indeed, William James, speaking about the flow of our own ideas says that “No object can catch our attention except by the neural machinery. But the amount of attention that it receives after it has caught our attention is another matter. It often takes effort to keep mind upon it.” [See Stapp, 2004, Sect. 12.7.4].
But how does quantum mechanics deal with the actions of the neural machinery, and more generally with what was happening at levels that are usually considered to lack any significant degree of mindfulness.
To better understand these ‘mechanical’ events, it is useful to consider first a standard ‘interference’ experiment. Suppose a photon falls upon a half-silvered mirror that transmits half the light falling upon it, and reflects the other half in a direction perpendicular to the transmitted beam. Suppose each of the two separated beams is then reflected at a right angle so that both fall on another half-silvered mirror that either transmits it, or reflects it at a right angle so that this ‘reflected’ part then lies on top of the ‘transmitted’ part of the beam coming from the other direction. One of the pair of two superposed beams exits the system and enters a 100% efficient detector D, and the other pair exits the system and enters a 100% efficient detector B.
Consider a photon detector DID that first detects with 100% efficiency, and then completely obliterates, any photon incident upon it. Suppose such a detector is placed on each of the two internal paths running between the two half-silvered mirrors. For each photon that enters this system one finds in principle---empirically confirmed within the expected experimental error---that either one or the other of these two internally placed detectors DID fires, each half the time. Moreover, these two detectors never both fire. Finally, each of the two detectors D and B that were placed in the output beams fires half the time, but never both D and B.
This set of results is exactly what is expected also from classical particle physics. However, if both internal detectors are removed, then for every photon that enters the system, the same external detector, called B for bright, fires once, and the other external detector, called D for dark, does not fire.
These features are all explained by the combined wave-particle aspects of quantum theory. But there is a ‘paradoxical’ feature. Placing a 100% efficient, and completely destructive, detector, DID, on just one of the two internal paths causes/allows the photon to go sometimes to D. Yet if the photon does go to D, then the DID whose placement in the beam allowed this to happen will necessarily be left in its initial unexcited state, completely unaffected.
One might try to explain this by saying that the photon simply definitely went one way other at each half-silvered mirror, and that the photon that arrived at D merely did not go to DID at the first half-silvered mirror, and then did not go to B at the second one. But if the photon definitely went either one way or the other at the first half-silvered mirror, then how does one understand the destructive interference between the two alternative paths to D if DID is not in place? How is the photon able to go just one way at the first half-silvered mirror, if and only if DID lies on one of its future possible paths, and, indeed, on a future path that it does not take. This is the puzzling particle-wave conundrum!
An even more puzzling/illuminating variation was devised by Kwait, Weinfurter, Herzog, and Zeilinger [1995]. The experiment that they did is equivalent ---as they note---to one that uses, instead of the two half-silvered mirrors, a sequence of N partially silvered mirrors each of which splits the beam amplitude into a reflected part that picks up a factor Cosine (π/2N) and a transmitted part that picks up a factor i Sine (π/2N). Both beams are then sent in opposite directions through the next partially silvered mirror, and so on, with each path that is ‘transmitted’ an even number of times going to external detector B, and each path that is ‘transmitted’ an odd number of times going to external detector D. One again finds that if no internal detector is put into the system then one of the two external detectors, namely B, will certainly fire, and other external detector, namely D, will certainly not fire. But if, for large N, a 100% efficient, and completely destructive, detector (a DID) is placed in each internal segment of the path that reaches D after being transmitted at the first beam splitter and being reflected at every other beam splitter, then for almost every photon that enters the apparatus the detector D will fire, instead of B, and none of the inserted DIDs will fire. So almost every photon that enters the system will be diverted, completely intact, from B to D by inserting these internal detectors DID, all of which will left completely unaffected by the diversion that they have caused.
According to the classical wave mechanical theory there would be, for any finite N, and for every entering pulse, no possibility that even one DID would be left completely unaffected, whereas according to quantum theory, for a large N, every DID will, for almost every entering photon pulse, be left completely unaffected. In the classical wave mechanical version, with the DIDs in place, every input pulse will emerge with less energy than it brought in, whereas according to quantum theory any pulse that exits the system will have all of the energy that it brought in. On the average, the two theories agree, but at the level of the individual quantum-sized pulses they are quite different.
The fact that for large finite N, with the DIDs in place, there is a large probability that the passage of the photon will leave each DID completely unaffected is a consequence of the quantum Zeno effect: the finely spaced ‘measurements’ tend to keep DIDs exactly in their original unexcited state.
The rationally coherent way to understand the quantum dynamics is to understand that the actual things are events located in regions, not moving objects. Placing detectors in region R modifies that region. It creates in R a potentiality for a certain kind of event either to occur there or not to occur there. For large N, there is a large likelihood that nothing at all occurs in that region R occupied by the DIDs, but that the photon energy is nevertheless, by virtue of the change made in the region R, forced to go to D instead of B. This conception of reality in terms of properties of regions to actualize or not actualize particular potentialities, in strict accordance with the statistical rules of quantum theory, is the core idea of the Quantum-Whiteheadian approach.
The example discussed above shows how, with a fairly high level of reliability, a fairly large amount of energy can, by changing the transmitivity of a region R, be diverted from B to D, without any effect at all upon either the amount of energy delivered to D at each detection event that occurs there, or upon the character of the region R. In the classical analog the each pulse arriving at D will have less energy than what it originally had, and each pulse will alter slightly the properties of R.
Insofar as the fundamentally quantum mechanical brain can evolve in a way that can usefully exploit these potentially available quantum mechanical features one might reasonably expect it to do so. Such a brain could be superior to a classical brain in the trial and error development of a repertory of useful templates for action: the fine tuning of transmitted energies and of properties of the medium can be important to the optimal functioning of a complex dynamical quantum system. (Consider the transmission of information via a photon emitted by an atom at one site and absorbed by the same kind of atom at another site) Also, “The quantum dynamics allows ‘optimal’ self-generating resonant states to emerge from the amorphous quantum soup with a certain maximal efficiency because all of the possible overlapping configurations of classical possibilities are simultaneously present, and their consequences are simultaneously explored by the quantum dynamics.” [Stapp, 1994, p. 288] Here ‘optimal’ means most likely to lead to the intended feedback. A reduction of the dynamics to a more classical dynamical level tends to disrupt the stability of the quantum-stabilized state. [Stapp, 1994, p.288]
According to Whitehead, each actual occasion must have some mental aspect. But the examples described above indicate that the laws of nature are such that a certain region can be treated as the locus of an actual quantum detection event, even though the physical properties located in that region would not warrant assigning any appreciable amount of conscious awareness to that region itself. Consequently, a biological system should be able to exploit the specific advantages of quantum dynamics discussed above, without necessarily harboring conscious awareness in any ordinary sense of the word.
The condition that, at some level, a particular detection event definitely either happens, or does not happen, (in accordance with the quantum probability rule) requires at that level some sort of discrete choice of one part of the wave-mechanical evolving state of the physically described universe. There is no empirical evidence for the entry of any element of discreteness before the entry of conscious awareness. It is therefore logically possible to maintain a purely mechanical determinism at all non-conscious levels of the universe by assuming, in accordance with both orthodox quantum mechanics and Whiteheadian philosophy, that any entry of a discrete choice occurs only in association with an aspect of nature having the character of conscious awareness, and to allow wave mechanical deterministic continuity to prevail in all mindless activity. That is, there is no logical need to introduce the notion of a discrete choice of one particular mechanically generated branch, from among many, before introducing the notion of a consciously aware mind.
On the other hand, as emphasized by the examples described above, quantum mechanics also allows regions presumably not supportive of conscious awareness to be treated as if they were loci of actual events/occasions, insofar as some future experience will effectively depend upon the choice specified by that actual event. This movability of the level at which the actualization events can be considered to occur was often emphasized by the founders of quantum mechanics, and was effectively demonstrated by von Neumann [1932/1955] in his theory of the process of ‘measurement’.
The bottom line is that one can use the basic quantum idea that a small region can actualizes potentialities created by earlier events, without assigning consciousness to that small region itself.
5. Classicality and Brain Process.
The question arises: Why should a quantum mechanically described brain produce classically describable conceptions of the physical world?
The quantum mechanical brain can be presumed to be represented by quantum electrodynamics, which deals with relationships between the motions of charged particles and changes of the electromagnetic field. This field has a class of states called ‘coherent states’ that have properties very similar to the properties of corresponding states of classical electromagnetic fields. [Klauder, 1968, 1985] They can be defined by averages over regions that are large compared to atoms, but are small compared to the whole brain. These states tend to be dynamically robust, and to obey the dynamical equations of classical electrodynamics. This robustness makes the reductions to these states the ideal candidates for the physical aspects of those events whose mental aspects populate our streams of consciousness. [Stapp, 1987, 1994].
This likely connection between our conscious thoughts and these quasi-classical states of the electromagnetic fields in our brains connects naturally to the notion that the neural correlates of our conscious thoughts are associated with the so-called 40 Hertz oscillations found in our brains.
The logical continuation of the this discourse on the effect of mind upon brain involves this proposed connection between the 40 Hertz brain waves and these quasi-classical states of the electromagnetic fields in our brains. This connection is discussed in three chapters of recent or soon-to-appear books [Stapp, 2009 a,b,c]. They focus particularly on the technical details of the bodily implementation of conscious intent through application of the quantum Zeno effect.
References
N. Bohr, Atomic Physics and Human Knowledge, New York: Wiley, 1958.
W. Heisenberg, “The Representation of Nature in Contemporary Physics”, in Daedalus 87 (summer), 95-108, 1958a.
W. Heisenberg, Physics and Philosophy, New York: Harper, 1958b.
P. Kwait, H. Weinfurter, T. Herzog, and A. Zeilinger, Interaction-Free Measurement, Phys. Rev. Letters 74, 4763-66, 1995.
J. von Neumann, Mathematical Foundations of Quantum Mechanics, Princeton N.J.: Princeton University Press, (translated from the Springer 1932 German original by Robert T. Beyers), 1955.
B. Russell, History of Western Philosophy, Simon and Schuster, 1945.
J. Schwinger, “Theory of Quantized Fields I”, Physical Review 82, 1951, pp. 914-927.
H.P. Stapp, Einstein Time and Process Time, in Physics and the Ultimate Significance of Time, ed, David R. Griffin, Albany: Suny Press, 1985.
H. P. Stapp, Quantum Mechanical Coherence, Resonance, and Mind, in Proceedings of Symposia in Applied Mathematics, Volume 52, Proceedings of the Norbert Wiener Centenary Congress. American Mathematical Society, 1994.
H.P. Stapp, Mind, Matter, and Quantum Mechanics, Second edition, Berlin, Heidelberg, New York: Springer, 2004
H. P. Stapp, Mindful Universe: Quantum Mechanics and the Participating Observer, Berlin, Heidelberg, New York: Springer, 2007.
H.P Stapp, Physicalism Versus Quantum Mechanics, in Mind, Matter, and Quantum Mechanics, Third edition, Berlin, Heidelberg, New York: Springer, Chapter 13, 2009a. (arxiv.org/abs/0803.1625)
H.P. Stapp, A Model of the Quantum-Classical and Mind-Brain Connections, and the Role of the Quantum Zeno Effect in the Physical Implementation of Conscious Intent, in Mind, Matter, and Quantum Mechanics, Third edition, Berlin, Heidelberg, New York: Springer, Chapter 14, 2009b (arxiv.org/abs/0803.1633)
H.P. Stapp, Philosophy of Mind and the Problem of Free Will in the Light of Quantum Mechanics, in On Thinking, Berlin, Heidelberg, New York: Springer, 2009b (arxiv.org/abs/0805.1633.0116)
S. Tomonaga, “On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields”, in Progress of Theoretical Physics 1, 1946, pp. 27-42.
J. von Neumann, Mathematical Foundations of Quantum Mechanics, Princeton: Princeton University Press. (Translated by Robert T. Beyer from the 1932 German original, Mathematiche Grundlagen der Quantummechanik. Berlin: J. Springer) 1932/1955